Variance de la population
Jusqu'à présent, nous avons travaillé sur des échantillons, c'est-à-dire sur quelques individus. Or, ce qui nous intéresse, c'est de tirer des conclusions sur une population qui serait représentée par cet échantillon.
On cherche donc à deviner, à partir de l'échantillon, quelle est la variabilité de la population. En réalité, la variance de l'échantillon n'est pas la meilleure estimation de la variance de la population (contrairement à la moyenne). Celle-ci est en fait donnée par la formule :
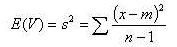
Le "-1" du dénominateur est appelé "correction de Bessel".
Pour comprendre la différence avec la formule de la variance de l'échantillon...
Prenons le problème à l'envers : nous avons vu qu'il fallait au minimum 1 individu dans notre échantillon pour estimer la moyenne de la population. Combien en faut-il pour estimer la variabilité de cette population ?
Un seul n'est pas suffisant. Alors que deux individus commencent à donner une idée de cette variabilité.
La formule nous permet de nous en rappeler : avec 1 individu dans l'échantillon, il n'y a pas de variabilité dans l'échantillon.
Etant donné que n=1, le dénominateur de la formule de ? est égal à 1; le numérateur est égal à la valeur de l'individu moins la moyenne (qui est également la valeur de l'individu puisqu'il est tout seul). Le résultat est donc (valeur-valeur)2/1=0, ce qui confirme qu'il n'y a pas de variabilité dans l'échantillon.
Mais cela ne signifie pas qu'il n'y a pas de variabilité dans la population. Si l'on cherche à estimer la variabilité de la population avec cette formule, on va penser que celle-ci est également nulle, ce qui est probablement faux.
Si, au contraire on utilise la formule de s2, le dénominateur (n-1) devient égal à 0 si on a qu'un seul individu dans l'échantillon et l'on constate qu'avec un seul individu dans l'échantillon, l'estimation de la variabilité de la population est impossible.
OK, ce n'est pas une démonstration mais plutôt un moyen simple de comprendre et de se rappeler quelle formule on doit utiliser : est-ce que ce qui m'intéresse, c'est l'échantillon que j'ai sous les yeux (30 patients sur lesquels je teste le sirop) ou la population qu'il représente (tous les patients de la terre susceptibles de prendre le sirop) ?
La variance de la population se note : E(V) (pour Estimation de la Variance de la population à partir de l'échantillon), S2 (pour EStimation), s2 (idem), ?2 (car certains statisticiens réservent les lettres grecques pour les populations et les lettres latines pour les échantillons),...
Fidèles à notre contrainte mnémotechnique, nous adopterons s2 pour noter l'EStimation de la variance de la population à partir de l'échantillon.
Nous arrivons ici au paroxysme de la divergence d'opinion concernant les notations. Toutes ont de bons arguments d'être choisies.
En tant que biologistes ou que psychologues, notre rôle n'est pas de dire qui a raison, mais d'être efficaces. En d'autres termes, nous devons comprendre toutes les notations qui peuvent se présenter en sachant que selon l'auteur, une même lettre peut vouloir dire deux choses différentes...
Page suivante : Ecart type de la population
Page précédente : Ecart type
Retour au plan
On cherche donc à deviner, à partir de l'échantillon, quelle est la variabilité de la population. En réalité, la variance de l'échantillon n'est pas la meilleure estimation de la variance de la population (contrairement à la moyenne). Celle-ci est en fait donnée par la formule :
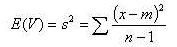
Le "-1" du dénominateur est appelé "correction de Bessel".
Pour comprendre la différence avec la formule de la variance de l'échantillon...
Prenons le problème à l'envers : nous avons vu qu'il fallait au minimum 1 individu dans notre échantillon pour estimer la moyenne de la population. Combien en faut-il pour estimer la variabilité de cette population ?
Un seul n'est pas suffisant. Alors que deux individus commencent à donner une idée de cette variabilité.
La formule nous permet de nous en rappeler : avec 1 individu dans l'échantillon, il n'y a pas de variabilité dans l'échantillon.
Etant donné que n=1, le dénominateur de la formule de ? est égal à 1; le numérateur est égal à la valeur de l'individu moins la moyenne (qui est également la valeur de l'individu puisqu'il est tout seul). Le résultat est donc (valeur-valeur)2/1=0, ce qui confirme qu'il n'y a pas de variabilité dans l'échantillon.
Mais cela ne signifie pas qu'il n'y a pas de variabilité dans la population. Si l'on cherche à estimer la variabilité de la population avec cette formule, on va penser que celle-ci est également nulle, ce qui est probablement faux.
Si, au contraire on utilise la formule de s2, le dénominateur (n-1) devient égal à 0 si on a qu'un seul individu dans l'échantillon et l'on constate qu'avec un seul individu dans l'échantillon, l'estimation de la variabilité de la population est impossible.
OK, ce n'est pas une démonstration mais plutôt un moyen simple de comprendre et de se rappeler quelle formule on doit utiliser : est-ce que ce qui m'intéresse, c'est l'échantillon que j'ai sous les yeux (30 patients sur lesquels je teste le sirop) ou la population qu'il représente (tous les patients de la terre susceptibles de prendre le sirop) ?
La variance de la population se note : E(V) (pour Estimation de la Variance de la population à partir de l'échantillon), S2 (pour EStimation), s2 (idem), ?2 (car certains statisticiens réservent les lettres grecques pour les populations et les lettres latines pour les échantillons),...
Fidèles à notre contrainte mnémotechnique, nous adopterons s2 pour noter l'EStimation de la variance de la population à partir de l'échantillon.
Nous arrivons ici au paroxysme de la divergence d'opinion concernant les notations. Toutes ont de bons arguments d'être choisies.
En tant que biologistes ou que psychologues, notre rôle n'est pas de dire qui a raison, mais d'être efficaces. En d'autres termes, nous devons comprendre toutes les notations qui peuvent se présenter en sachant que selon l'auteur, une même lettre peut vouloir dire deux choses différentes...
Page suivante : Ecart type de la population
Page précédente : Ecart type
Retour au plan
A découvrir aussi
- Etapes d'une ANOVA à 2 facteurs
- ANOVA 1 facteur : exemple d'analyse
- Déroulement d'une ANOVA à 1 facteur
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres