L'écart type
Nous avons vu que la variance ne représentait pas grand chose sur le graphique. Aussi, pour rendre ce paramètre un peu plus parlant, on peut en calculer la racine carrée. C'est l'écart type.
La formule en est donc :
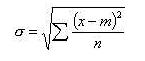
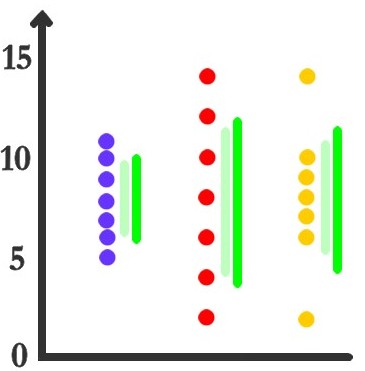
L'écart type est en vert vif. En vert pâle, j'ai reproduit la moyenne des écarts à la moyenne. On obtient donc deux indices relativement parlants de la variabilité dans un échantillon.
Selon les auteurs, l'écart type se note :
σ, racine(V), [s, qui peut prêter à confusion, de même que σ], SD (pour standard deviation en anglais).
Nous utiliserons σ par la suite.
Page suivante : Variance de la population
Page précédente : Variance
Retour au plan
La formule en est donc :
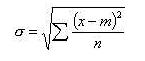

L'écart type est en vert vif. En vert pâle, j'ai reproduit la moyenne des écarts à la moyenne. On obtient donc deux indices relativement parlants de la variabilité dans un échantillon.
Selon les auteurs, l'écart type se note :
σ, racine(V), [s, qui peut prêter à confusion, de même que σ], SD (pour standard deviation en anglais).
Nous utiliserons σ par la suite.
Page suivante : Variance de la population
Page précédente : Variance
Retour au plan
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres