La question que l'on se pose
Vous avez administré une substance supposée améliorer la mémoire à un groupe expérimental de sujets (souris, humains...) et comparez les performances mnésiques de ce groupe à celles d'un groupe témoin.
La substance est-elle réellement promnésiante ?
Que concluez-vous si vous obtenez ces résultats ? (cas 1)
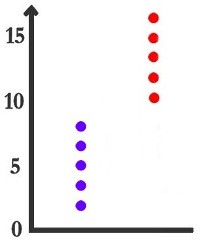
Que concluez-vous si vous obtenez ces résultats ? (cas 2)
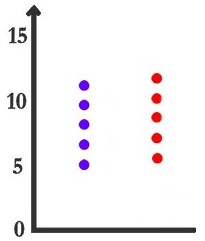
Que concluez-vous si vous obtenez ces résultats ? (cas 3)

Dans le cas 1, vous avez probablement conclu que la drogue avait l'effet supposé. Dans le cas 2, la drogue ne semble pas avoir d'effet. Enfin, dans le cas 3... vous avez peut-être conclu dans un sens ou dans l'autre. Vous n'avez peut-être pas osé conclure. Vous reconnaîtrez au moins que la décision à prendre est plus difficile que dans les cas 1 et 2.
Quelle question se pose-t-on réellement dans ces trois cas ?
Sans contestation possible, dans les trois cas la moyenne du groupe traité est toujours supérieure à celle du groupe témoin. La question que l'on se pose n'est donc pas : "la moyenne du groupe traité est-elle supérieure à celle des témoins ?".
A quoi la différence de moyennes peut-elle être due si ce n'est pas à l'influence de la drogue ? Intuitivement, nous l'attribuons aux fluctuations du hasard, au hasard de l'échantillonnage... On n'est pas étonné que les deux moyennes ne soient jamais strictement identiques car on accepte implicitement que le hasard de l'échantillonnage provoque cette différence de moyenne.
Ainsi, la véritable question que l'on se pose lorsque l'on regarde le cas 3 est :"la différence de moyennes que j'observe peut-elle être due au hasard ?".
Quand je regarde le cas 1, je me pose la même question, mais la réponse est tellement évidente que je n'ai pas le temps de prendre conscience que je me pose une question. Une telle différence ne peut pas être due au hasard; c'est donc l'effet de la drogue.
Dans le cas 2, il en est de même mais dans l'autre sens : "une si petite différence a tellement de chances d'être provoquée par le hasard que je préfère ne pas l'attribuer à l'effet de la drogue".
Reformulons plusieurs fois la question pour le cas 3 :
- la différence de moyennes que j'observe peut-elle être due au hasard ?
- quelle est le risque pour que la différence de moyennes que j'observe soit due au hasard ?
- quelle sont les chances pour que la différence de moyennes que j'observe soit due au hasard ?
encore une dernière formulation synonyme :
- quelle est la probabilité pour que la différence de moyennes que j'observe soit due au hasard ?
Si cette probabilité est faible, je conclurai que c'est la drogue qui a provoqué la différence.
Si elle est forte, je préférerai rester prudent et dire que l'expérience ne permet pas de démontrer que la drogue a un effet.
Quoi qu'il en soit nous avons tous les éléments pour inventer notre premier test statistique...
Page suivante : La roulette de Monte-Carlo
Page précédente : Interaction entre trois variables
Retour au plan
Quelle question se pose-t-on réellement dans ces trois cas ?
Sans contestation possible, dans les trois cas la moyenne du groupe traité est toujours supérieure à celle du groupe témoin. La question que l'on se pose n'est donc pas : "la moyenne du groupe traité est-elle supérieure à celle des témoins ?".
A quoi la différence de moyennes peut-elle être due si ce n'est pas à l'influence de la drogue ? Intuitivement, nous l'attribuons aux fluctuations du hasard, au hasard de l'échantillonnage... On n'est pas étonné que les deux moyennes ne soient jamais strictement identiques car on accepte implicitement que le hasard de l'échantillonnage provoque cette différence de moyenne.
Ainsi, la véritable question que l'on se pose lorsque l'on regarde le cas 3 est :"la différence de moyennes que j'observe peut-elle être due au hasard ?".
Quand je regarde le cas 1, je me pose la même question, mais la réponse est tellement évidente que je n'ai pas le temps de prendre conscience que je me pose une question. Une telle différence ne peut pas être due au hasard; c'est donc l'effet de la drogue.
Dans le cas 2, il en est de même mais dans l'autre sens : "une si petite différence a tellement de chances d'être provoquée par le hasard que je préfère ne pas l'attribuer à l'effet de la drogue".
Reformulons plusieurs fois la question pour le cas 3 :
- la différence de moyennes que j'observe peut-elle être due au hasard ?
- quelle est le risque pour que la différence de moyennes que j'observe soit due au hasard ?
- quelle sont les chances pour que la différence de moyennes que j'observe soit due au hasard ?
encore une dernière formulation synonyme :
- quelle est la probabilité pour que la différence de moyennes que j'observe soit due au hasard ?
Si cette probabilité est faible, je conclurai que c'est la drogue qui a provoqué la différence.
Si elle est forte, je préférerai rester prudent et dire que l'expérience ne permet pas de démontrer que la drogue a un effet.
Quoi qu'il en soit nous avons tous les éléments pour inventer notre premier test statistique...
Page suivante : La roulette de Monte-Carlo
Page précédente : Interaction entre trois variables
Retour au plan
A découvrir aussi
- Objectifs de la formation
- Première solution : inventons la roulette de Monte-Carlo
- Intérêt de cette typologie et de la connaissance des statuts
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 74 autres membres