NeuropsychoJolly (roger)

Répondre à la question "La population étudiée est-elle normale ?" consiste à se demander si la population dont est extrait l'échantillon suit une loi normale, ou, en d'autres termes, si les individus qui la constituent sont répartis selon une distribution normale.
La distribution est synonyme de répartition.
La normalité est une forme de répartition que l'on rencontre très fréquemment dans la nature : si vous classez des individus selon un paramètre (l'intelligence, la rapidité...) vous pourrez faire une moyenne, vous vous apercevrez qu'un grand nombre d'individus ont un "score" voisin de cette moyenne et plus on s'éloigne de cette moyenne, moins on trouve d'individus.

Pour certains tests statistiques il est nécessaire que les populations étudiées soient normales (en ce qui concerne la VD étudiée) sans quoi les résultats qu'ils donnent peuvent être faussés.
Il est important de noter que ce sont les populations dont sont extraits les échantillons qui doivent être normales et non les échantillons eux-mêmes.

Evidemment, le problème est que l'on dispose d'échantillons, mais pas de la population.

Comment savoir si la population est normale ?
Une variable qui suit une loi normale est symétrique autour de sa moyenne, présente de nombreuses valeurs près de sa moyenne, de moins en moins au fur et à mesure qu'on séloigne de cette moyenne. En théorie, une variable qui suit une loi normale peut prendre des valeurs infiniment petites ou grandes, ou plus exactement, elle n'est limitée ni par le haut, ni par le bas.
On sait qu'on ne trouvera pas sur terre une personne mesurant 25m, et pourtant aucune limite n'est fixée; le record actuel peut toujours être bâttu.

On voit ici un exemple de distribution normale:




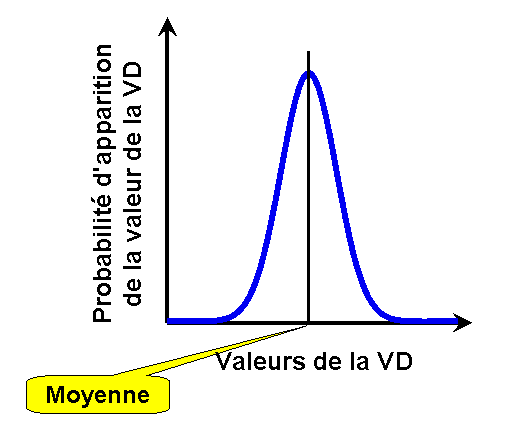
Je suggère 4 méthodes :

1) La méthode "théorique/intuitive"
Elle consiste à se demander si, a priori, il y a un risque pour que la population ne soit pas normale, c'est à dire soit bornée par le haut ou par le bas, ce qui entraînerait une dissymétrie. Si tel est le cas, la ou les bornes risquent-elles de provoquer cette dissymétrie ?
Entrainez-vous ici

2) La méthode graphique
Elle consiste considérer que l'échantillon représente bien la population, et donc que la distribution des individus représente celle de la population.
Si la distribution des individus présente un "sommet" au centre et une diminution progressive de chaque côté, on considérera que la distribution de la population est normale.
Entrainez-vous ici

3) Les indicateurs numériques
Il existe des indicateurs numériques de symétrie (index "Skewness") et "d'applatissement" (index "Kurtosis"). Ces deux indicateurs sont disponibles dans les "fonctions" d'Excel. De même, dans l'aide d'Excel, on trouvera les formules qui permettent de dire si une distribution s'éloigne trop de la symétrie ou si son applatissement est trop mauvais pour pouvoir considérer qu'elle suit une loi normale.

4) Les tests statistiques
Ils ont l'avantage de donner un apparence très sérieuse à l'étude mais sont finalement peu utilisables car dans nos disciplines expérimentales, nous disposons de trop peu de sujets pour pouvoir les utiliser.
On dispose du Khi2 pour comparaisons de distributions (il nécessite au moins 30 à 40 sujets par groupe...)
Le Kolmogorov-Smirnov pour comparaisons de distributions (aussi appelé test de Lillefors) peut également être utilisé et nécessite moins de sujets mais est peu puissant.
On trouve aussi dans la littérature les :
Test de Shapiro-Wilks
Test de Anderson-Darling
Test de Shapiro-Francia
D de D'Agostino
T de Spiegelhalter
I de Martin-Iglewicz
Liste non limitative...
J'avoue que je ne connais pas les subtilités de chacun de ces derniers tests.

Personnellement, j'utilise la méthode "théorique/intuitive", éventuellement complétée par la méthode graphique, les indicateurs numériques ne faisant que confirmer ce qui se voit. Eventuellement, ces indicateurs ainsi que les tests statistiques de normalité peuvent être utilisés pour convaincre un referee incrédule.