NeuropsychoJolly (roger)

Le coefficient de corrélation

Le but de la corrélation est de savoir s'il existe une relation entre deux variables, en d'autres termes si les individus qui ont des notes élevées sur une variable ont également des notes élevées sur une autre variable (cas de la corrélation positive; cf. graphique a). Une autre forme de relation est le cas où des sujets qui ont des notes élevées sur une variable ont des notes faibles sur une autre variable (cas de la corrélation négative; cf. graphique b).

En général, cette relation peut être mesurée par un coefficient de corrélation de Pearson (également appelé "de Bravais-Pearson") et noté "r".



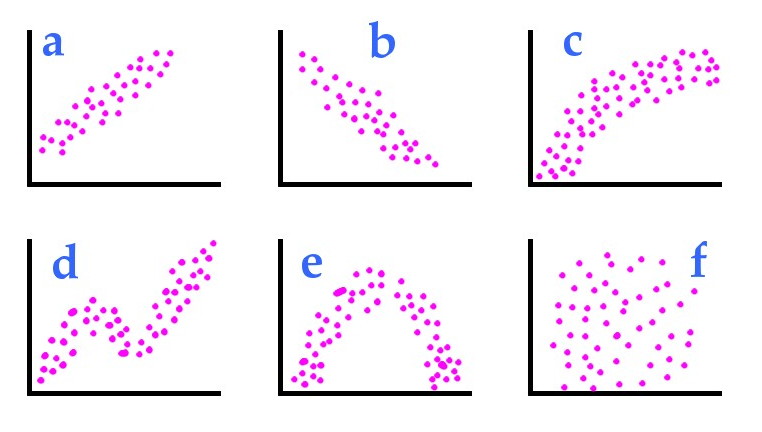
En théorie, r peut être utilisé pour mesurer des relations linéaires (cf. graphiques a et b).
En pratique, r peut détecter la plupart des relations "globalement monotones" (c'est-à-dire globalement  croissantes ou globalement décroissantes (cf. graphiques a, b, c et d), bien qu'il ne soit prévu que pour les relations linéaires et donc monotones. Mais dans la réalité de l'expérimentation, si on connaissait toujours la forme de la relation avant de faire l'expérience… on ne ferait pas l'expérience.

r est toujours compris entre -1 et +1
r = 0 ou voisin de 0 signifie une absence de relation (cf. graphiques f) ou une relation qui, globalement, n'est ni croissante ni décroissante (cf l'exemple classique de la relation entre motivation et performance, graphique e; un sujet non motivé a de mauvaises performances; un sujet trop motivé risque d'être trop stressé et donc d'avoir de mauvaises performances; un sujet motivé "normalement aura les meilleures performances);
r < 0 : une relation négative (plus je cours vite, moins je vois le paysage et inversement; cf. graphique b);
r > 0 : une relation positive (plus je cours vite, plus j'ai soif; cf. graphiques a ou c);
r = 1 ou r = -1 : relation linéaire parfaite (cf. graphiques a ou b mais où tous les points seraient parfaitement alignés).


Signification statistique d'un coefficient de corrélation

Si chacune des deux variables suit une distribution normale, on peut calculer la signification statistique du coefficient de corrélation, c'est-à-dire la probabilité d'obtenir un r aussi élevé (en valeur absolue), par hasard, s'il n'existe pas de relation réelle entre les deux variables.
Si cette probabilité est forte, on considère que le r n'est pas significatif (la relation est peut-être due aux aléas de l'échantillonnage), si elle est faible, on considérera qu'il est trop improbable d'obtenir un tel r par hasard, on considère donc qu'il reflète une relation réelle.
La signification statistique dépend de la valeur de r et du nombre de sujets "n", qui permet de calculer un "degré de liberté" : ddl = n - 2.

Si au moins une des deux variables ne suit pas une loi normale, le risque d'erreur alpha sera faussé.
S'il existe une relation non linéaire, le risque d'erreur alpha sera surestimé.
Dans ces deux cas, il sera préférable :
- en priorité : tenter de transformer la (ou les) variable(s) non normales. Cf. "Transformation"
- si cette opération s'avère inefficace, on préférera transformer les deux variables en variables ordinales et utiliser un coefficient de corrélation par rangs tel que le "rho de Spearman" ou le "tau de Kendal".

Si le coefficient de corrélation vous a plu, vous pouvez le mettre au carré, vous obtiendrez le pourcentage de variance expliquée... A faire Lien a faire

Hypothèses unilatérales et bilatérales
En général, les logiciels statistiques donnent les probabilités bilatérales. Si votre étude théorique qui précède et donne lieu aux expériences vous conduit à une hypothèse forte (qui précise le signe de la corrélation attendue), vous devez formuler une hypothèse unilatérale. Les probabilités de risque d'erreur alpha données par le logiciel devront alors être divisées par 2. Dans un tableau comprenant plusieurs variables, la théories peut vous mener à formuler des hypothèses unilatérales pour certaines corrélations, et bilatérales pour d'autres.


Exemple d'un monde dans lequel les gens bons sont bons partout
Pour chaque sujet (1 sujet par ligne), la première note est celle de maths, la seconde celle de français.

1, 1
3, 3
4, 3
5, 4
5, 5
6, 4
6, 6
6, 8
7, 7
8, 6
8, 9
8, 10
9, 12
10, 12
12, 11

Sur un tableur, on peut entrer les notes de math dans une colonne (par exemple colonne B), celle de français dans une autre (par exemple colonne C). Dans une cellule, on colle la fonction :

=COEFFICIENT.CORRELATION(B1:B15;C1:C15)

On trouve 0.90637…; c'est le coefficient de corrélation.

Avec un logiciel statistique, on obtiendra en général le résultat sous forme de "matrice triangulaire" (c'est-à-dire de tableau comme ci-dessous). De plus, on peut demander la "signification statistique" du coefficient de corrélation (cf. "Matrix of Probabilities").

************************************
Pearson correlation matrix   
                 MATH       FRANCAIS
MATH            1.000 
FRANCAIS        0.906        1.000


Matrix of Probabilities    
                 MATH       FRANCAIS
MATH            0.000   
FRANCAIS        0.000        0.000 

Number of observations: 15
************************************

D'après ces tableaux, le coefficient de corrélation entre les notes de math et de français est r = 0.906; cette relation  est significative (p < 0.001). (Le risque d'obtenir un coefficient de corrélation de 0.906 par hasard lorsque l'on a 15 sujets et qu'il n'y a en réalité pas de lien entre les notes de math et de français est inférieur à 1 pour mille.

Un intérêt des logiciels statistiques, est qu'ils permettent de calculer plusieurs coefficients de corrélation simultanément. La notion de matrice prend alors tout son sens.
Introduisons par exemple la pointure de l'élève dans le tableau et le nombre de punitions reçues dans l'année.

************************************

Pearson correlation matrix
              MATH    FRANCAIS    POINTURE    PUNITIONS
MATH         1.000           
FRANCAIS     0.906       1.000       
POINTURE    -0.113      -0.022       1.000   
PUNITIONS   -0.627      -0.695      -0.120        1.000
 
Bartlett Chi-square statistic:    29.240 df=6 Prob= 0.000
 
Matrix of Probabilities
              MATH    FRANCAIS    POINTURE    PUNITIONS
MATH         0.000           
FRANCAIS     0.000       0.000       
POINTURE     0.688       0.939       0.000   
PUNITIONS    0.012       0.004       0.671        0.000
 
Number of observations: 15
 
************************************

On note par exemple que la corrélation entre la pointure et le nombre de punitions est de -0.12, ce qui signifie que ceux qui ont de grand pieds ont moins de punitions... Mais le tableau des probabilités indique que le risque d'erreur alpha est de 0.671, ce qui signifie que s'il n'y a en réalité pas de relation entre ces deux paramètres, la probabilité d'obtenir une corrélation de -0.12 est de 67,1%. On ne peut donc pas considérer (au risque d'erreur alpha de 5% qu'il y a un lien entre la taille des pieds et le nombre de punitions.

Etant donné que nous effectuons 6 tests statistiques, nous risquons de voir apparaître des différences significatives, simplement par hasard. Il peut être bon d'apporter une correction de Bonferroni à ces tests. Certains logiciels offrent cette possibilité (je prédis que je vais faire un 6 avec mon dé... si je ne triche pas, il n'y a qu'une chance sur 6 que je réussisse. mais si je recommence l'expérience plusieurs fois, la prédiction va finir par se réaliser. Celà signifie-t-il que je peux lire l'avenir ?... Bonferroni corrige ce biais).

************************************

Pearson correlation matrix
              MATH     FRANCAIS    POINTURE    PUNITIONS
MATH         1.000           
FRANCAIS     0.906        1.000       
POINTURE    -0.113       -0.022       1.000   
PUNITIONS   -0.627       -0.695       -0.120       1.000
 
Bartlett Chi-square statistic:    29.240 df=6 Prob= 0.000
 
Matrix of Bonferroni Probabilities
              MATH    FRANCAIS    POINTURE    PUNITIONS
MATH         0.000           
FRANCAIS     0.000       0.000       
POINTURE     1.000       1.000       0.000   
PUNITIONS    0.074       0.024       1.000        0.000
 
Number of observations: 15
 
************************************

On constate qu'avec Bonferroni, les risques d'erreurs alpha sont plus élevés. Par exemple, le risque d'erreur alpha de la corrélation entre français et punitions était de 0.004 sans correction; il passe à 0.024 avec Bonferroni. Nous notons également que la relation maths / punitions n'est plus significative.

Mais un petit travail théorique aurait permi à ce chercheur de se dire que les performances en maths et en français étaient probablement liées de façon positive à la discipline que s'impose chaque élève et donc de façon négative au nombre de punitions. Le chercheur aurait alors pu a priori formuler une hypothèse unilatérale (ex : le coefficient de corrélation entre math et punitions est négatif). La probabilité est alors à diviser par 2 : p=0,037. Il peut alors conclure que la relation entre le nombre de punitions et les performances en maths est significative (0,037<0,05).

Mais avouez qu'il était un peu stupide de chercher une corrélation entre des performances en épreuves intellectuelles, les punitions (pouvant reflèter un niveau d'auto-discipline) d'une part,  et la taille des pieds d'autre part. Reprenons l'analyse sans la taille des pieds.

************************************

Pearson correlation matrix
             MATH    FRANCAIS    PUNITIONS
MATH        1.000       
FRANCAIS    0.906       1.000   
PUNITIONS  -0.627      -0.695        1.000
 
Bartlett Chi-square statistic:    28.996 df=3 Prob= 0.000
 
Matrix of Bonferroni Probabilities
             MATH    FRANCAIS    PUNITIONS
MATH        0.000       
FRANCAIS    0.000       0.000   
PUNITIONS   0.037       0.012        0.000
 
Number of observations: 15

************************************

La corrélation entre maths et punitions redevient significative (p=0.037, ce qui est inférieur à 0.05, seuil de signification).
De plus, avec une hypothèse unilatérale, p(alpha)=0,0185



Moralité :

- Si vous voulez être rigoureux, utilisez la correction de BONFERRONI lorsque vous multipliez les tests statistiques dans une même expérience,

- Pour augmenter la puissance de vos tests, clarifiez et précisez vos hypothèses grâce à un travail théorique AVANT de faire les expériences,

- Pour augmenter la puissance de vos tests, n'introduisez dans vos analyses QUE des variables dont la présence est JUISTIFIEE PAR LA THEORIE.