La correction de Bonferroni
NB : D'après Wikipedia, on devrait dire "Dunn-Bonferroni", mais dans d'autres manuels, on trouve également les orthographes : "Benferroni", "Benferoni" et "Bonferoni".
Comment fait-on ? (le quand et le pourquoi viendront juste après)
Avant l'analyse statistique, voire avant l'expérience,
- on choisit le seuil de risque d'erreur alpha à partir duquel on considère la différence significative (alpha),
- on planifie (on prévoie) les comparaisons qui vont être faites,
- on compte le nombre (k) de tests qui vont être faits (le plus souvent, il s'agit de comparaisons),
- on se demande si les résultats des tests vont être indépendants ou s'ils vont dépendre les uns des autres.
Après l'expérience,
- on effectue les tests statistiques (t de Student, coefficient de corrélation...). On les utilise pour effectuer les comparaisons prévues, et seulement celles-là.
- On obtient des "probabilités de risque d'erreur alpha". Par exemple : p=0.0025; p=0.123; p=0.048
- On corrige ces probabilités :
Si les résultats des tests sont indépendants on calcule
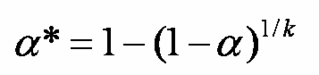
(D'après Wikipedia, cette correction devrait être appelée "correction de Sidak" ou "correction de "Dunn-Sidak").
Si les résultats des tests sont interdépendants on calcule
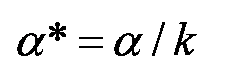
"k" est le nombre de comparaisons effectuées
"alpha" est le seuil de risque d'erreur alpha à partir duquel on considère la différence significative
On trouve "alpha*".
Si la probabilité p est inférieure ou égale à alpha* alors on considère que le test (la comparaison...) est significatif au risque d'erreur alpha. Sinon, le test n'est pas significatif.
Exemple : j'effectue trois comparaisons avec des tests indépendants.
Seuil choisi : alpha = 5%
Résultats au test t de Student : p=0.0025; p=0.123; p=0.048
Alpha* = 0.01695243
Première comparaison : p=0.0025 < 0.01695
Le résultat est significatif au risque d'erreur alpha de 5%
Deuxième comparaison : p=0.123 > 0.01695
Le résultat n'est pas significatif au risque d'erreur alpha de 5%
Troisième comparaison : p=0.048 > 0.01695
Le résultat n'est pas significatif au risque d'erreur alpha de 5%
Quand des tests sont-ils indépendants; quand sont-ils interdépendants
Les tests sont indépendants lorsque le résultat de l'un ne permet pas du tout de prédire le résultat de l'autre. Exemple : je compare la rapidité des enfants dans une tâche à celle des adultes puis la rapidité des adultes à celle des personnes agées.
Les tests sont inter-dépendants lorsque le résultat de l'un peut permettre de prédire le résultat de l'autre. Exemple : je sais qu'un ensemble de neurones (A) active un autre ensemble de neurones (B). J'étudie l'effet d'une substance. Le premier test montre qu'elle active significativement l'ensemble A. Je peux me douter que l'ensemble B va également être activé.
Si on a un doute, on calcule les deux alpha* et on garde celui qui a la valeur la plus élevée.
Quand ?
La correction de Bonferroni peut s'appliquer à n'importe quel test statistique (t de Student, coefficients de corrélations,...), c'est une façon de corriger l'erreur commise sur le risque d'erreur alpha lorsque l'on utilise plusieurs fois le même test.
Bonferroni est un test a priori. Cela signifie qu'il est inutile de faire une ANOVA avant.
Dans le cas d'un plan expérimental incomplet de type ANOVA à plusieurs facteurs. Un plan incomplet est un plan dans lequel il manquerait au moins un groupe. On remplace alors les ANOVAs par des t de Student corrigés par Bonferroni. Un plan incomplet est soit la conséquence d'une erreur dans la conception de l'expérience, soit d'un événement non prévu : mort de tous les sujets d'un groupe, destruction des données d'un groupe...
Dans le cas d'un plan expérimental trop compliqué (4 facteurs ou plus, trop de modalités...). Il s'agit alors de "rattraper" un plan d'expérience mal conçu.
J'ai été amené à concevoir un plan incomplet :
Un test comportemental a été validé sur des souris jeunes de souche Balb/c (Blanches albinos). Ces souris sont difficiles à faire vieillir; on leur préfère la souche C57Bl6 (noires; Bl = black).
Pour travailler sur le viellissement il a fallu changer de souche et valider le test sur cette nouvelle souche.
Le plan avait donc 2 facteurs : 1 facteur "âge" (modalités "jeunes" et "vieilles") et 1 facteur souche (modalités "blanches" et "noires").
Les blanche vieillissant mal, l'expérience ne pouvait être constituée que de 3 groupes : "jeunes blanches", "jeunes noires", "vieilles noires" et il manquait le groupe "vieilles blanches" pour avoir un plan complet.
La solution consistait à comparer les trois groupes entre eux par une ANOVA + post-hocs en constituant 1 seul facteur groupe à 3 modalités ("jeunes blanches", "jeunes noires", "vieilles noires"), ou alors à comparer directement "jeunes blanches" avec "jeunes noires" puis "jeunes noires" avec "vieilles noires" (2 comparaisons) avec des t de Student, puis à effectuer la correction de Bonferroni. On évite alors de comparer les "jeunes blanches" avec les "vieilles noires" car cette comparaison n'a pas vraiment d'utilité scientifique et qu'une comparaison supplémentaire fait perdre de la puissance au test lors de la correction de Bonferroni.
On évitera de l'utiliser :
Dans le cas d'un plan expérimental de type ANOVA à 1 facteur à plus de 2 modalités, on peut remplacer l'ANOVA + tests post-hoc (Tukey, Neuman-Keuls, Dunnett) par des t de Student corrigés par Bonferroni, mais en général l'ANOVA + post-hocs est plus puissante.
Pourquoi ?
Admettons que le traitement que je donne à des sujets (pour les rendre plus intelligents) n'ait pas d'effet, mais je ne le sais pas. Je dois donc vérifier expérimentalement que le traitement a un effet.
Je constitue 1 groupe recevant la drogue et 1 groupe placebo.
Il y a de fortes chances pour que les groupes aient un résultat à peu près identique. Je refais l'expérience : même résultat. Je refais l'expérience plusieurs fois. Au bout d'un certain temps, par hasard, sur une expérience, le groupe traité apparaîtra plus intelligent que l'autre. Faut-il conclure que la drogue a un effet ?
La correction de Bonferroni se base sur un calcul de probabilité pour éviter ce risque.
De la même manière, si je compare les effets de 15 substances (qui n'ont en réalité pas d'effet, ce que l'on ne sait pas a priori) à un témoin, il y a des chances non négligeables pour qu'une ou deux "sortent du lot" par hasard. Bonferroni corrige cela.
Idée fausse et autres idées
"Une ANOVA doit précéder les comparaisons corrigées par Bonferroni".
En réalité, une ANOVA doit absolument précéder les comparaisons menées avec un test de Fisher PPDS (Plus Petite Différence Significative; "Fisher LSD" pour "Least Significant Difference" en anglais) qui est un test test "post-hoc" ou "a posteriori", mais pas la correction par Bonferroni qui est une procédure "a priori" basée sur un calcul de probabilités. Mais un grand nombre "d'experts" pour revues scientifiques l'ignorent.
Les tests de Tukey, Neuman-Keuls et Dunnett sont considérés comme tests a posteriori (et ne sont effectués qu'après une ANOVA préalable), mais d'après Zar (1999) cette ANOVA préalable ne se justifie pas en raison de la théorie sur laquelle ils sont basés...
Biblio
Zar JH. 1999. Biostatistical analysis. Fourth Ed. Prentice Hall, Upper Saddle River, New Jersey. pp663.
Comment fait-on ? (le quand et le pourquoi viendront juste après)
Avant l'analyse statistique, voire avant l'expérience,
- on choisit le seuil de risque d'erreur alpha à partir duquel on considère la différence significative (alpha),
- on planifie (on prévoie) les comparaisons qui vont être faites,
- on compte le nombre (k) de tests qui vont être faits (le plus souvent, il s'agit de comparaisons),
- on se demande si les résultats des tests vont être indépendants ou s'ils vont dépendre les uns des autres.
Après l'expérience,
- on effectue les tests statistiques (t de Student, coefficient de corrélation...). On les utilise pour effectuer les comparaisons prévues, et seulement celles-là.
- On obtient des "probabilités de risque d'erreur alpha". Par exemple : p=0.0025; p=0.123; p=0.048
- On corrige ces probabilités :
Si les résultats des tests sont indépendants on calcule
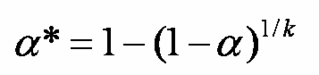
(D'après Wikipedia, cette correction devrait être appelée "correction de Sidak" ou "correction de "Dunn-Sidak").
Si les résultats des tests sont interdépendants on calcule
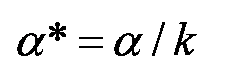
"k" est le nombre de comparaisons effectuées
"alpha" est le seuil de risque d'erreur alpha à partir duquel on considère la différence significative
On trouve "alpha*".
Si la probabilité p est inférieure ou égale à alpha* alors on considère que le test (la comparaison...) est significatif au risque d'erreur alpha. Sinon, le test n'est pas significatif.
Exemple : j'effectue trois comparaisons avec des tests indépendants.
Seuil choisi : alpha = 5%
Résultats au test t de Student : p=0.0025; p=0.123; p=0.048
Alpha* = 0.01695243
Première comparaison : p=0.0025 < 0.01695
Le résultat est significatif au risque d'erreur alpha de 5%
Deuxième comparaison : p=0.123 > 0.01695
Le résultat n'est pas significatif au risque d'erreur alpha de 5%
Troisième comparaison : p=0.048 > 0.01695
Le résultat n'est pas significatif au risque d'erreur alpha de 5%
Quand des tests sont-ils indépendants; quand sont-ils interdépendants
Les tests sont indépendants lorsque le résultat de l'un ne permet pas du tout de prédire le résultat de l'autre. Exemple : je compare la rapidité des enfants dans une tâche à celle des adultes puis la rapidité des adultes à celle des personnes agées.
Les tests sont inter-dépendants lorsque le résultat de l'un peut permettre de prédire le résultat de l'autre. Exemple : je sais qu'un ensemble de neurones (A) active un autre ensemble de neurones (B). J'étudie l'effet d'une substance. Le premier test montre qu'elle active significativement l'ensemble A. Je peux me douter que l'ensemble B va également être activé.
Si on a un doute, on calcule les deux alpha* et on garde celui qui a la valeur la plus élevée.
Quand ?
La correction de Bonferroni peut s'appliquer à n'importe quel test statistique (t de Student, coefficients de corrélations,...), c'est une façon de corriger l'erreur commise sur le risque d'erreur alpha lorsque l'on utilise plusieurs fois le même test.
Bonferroni est un test a priori. Cela signifie qu'il est inutile de faire une ANOVA avant.
Dans le cas d'un plan expérimental incomplet de type ANOVA à plusieurs facteurs. Un plan incomplet est un plan dans lequel il manquerait au moins un groupe. On remplace alors les ANOVAs par des t de Student corrigés par Bonferroni. Un plan incomplet est soit la conséquence d'une erreur dans la conception de l'expérience, soit d'un événement non prévu : mort de tous les sujets d'un groupe, destruction des données d'un groupe...
Dans le cas d'un plan expérimental trop compliqué (4 facteurs ou plus, trop de modalités...). Il s'agit alors de "rattraper" un plan d'expérience mal conçu.
J'ai été amené à concevoir un plan incomplet :
Un test comportemental a été validé sur des souris jeunes de souche Balb/c (Blanches albinos). Ces souris sont difficiles à faire vieillir; on leur préfère la souche C57Bl6 (noires; Bl = black).
Pour travailler sur le viellissement il a fallu changer de souche et valider le test sur cette nouvelle souche.
Le plan avait donc 2 facteurs : 1 facteur "âge" (modalités "jeunes" et "vieilles") et 1 facteur souche (modalités "blanches" et "noires").
Les blanche vieillissant mal, l'expérience ne pouvait être constituée que de 3 groupes : "jeunes blanches", "jeunes noires", "vieilles noires" et il manquait le groupe "vieilles blanches" pour avoir un plan complet.
La solution consistait à comparer les trois groupes entre eux par une ANOVA + post-hocs en constituant 1 seul facteur groupe à 3 modalités ("jeunes blanches", "jeunes noires", "vieilles noires"), ou alors à comparer directement "jeunes blanches" avec "jeunes noires" puis "jeunes noires" avec "vieilles noires" (2 comparaisons) avec des t de Student, puis à effectuer la correction de Bonferroni. On évite alors de comparer les "jeunes blanches" avec les "vieilles noires" car cette comparaison n'a pas vraiment d'utilité scientifique et qu'une comparaison supplémentaire fait perdre de la puissance au test lors de la correction de Bonferroni.
On évitera de l'utiliser :
Dans le cas d'un plan expérimental de type ANOVA à 1 facteur à plus de 2 modalités, on peut remplacer l'ANOVA + tests post-hoc (Tukey, Neuman-Keuls, Dunnett) par des t de Student corrigés par Bonferroni, mais en général l'ANOVA + post-hocs est plus puissante.
Pourquoi ?
Admettons que le traitement que je donne à des sujets (pour les rendre plus intelligents) n'ait pas d'effet, mais je ne le sais pas. Je dois donc vérifier expérimentalement que le traitement a un effet.
Je constitue 1 groupe recevant la drogue et 1 groupe placebo.
Il y a de fortes chances pour que les groupes aient un résultat à peu près identique. Je refais l'expérience : même résultat. Je refais l'expérience plusieurs fois. Au bout d'un certain temps, par hasard, sur une expérience, le groupe traité apparaîtra plus intelligent que l'autre. Faut-il conclure que la drogue a un effet ?
La correction de Bonferroni se base sur un calcul de probabilité pour éviter ce risque.
De la même manière, si je compare les effets de 15 substances (qui n'ont en réalité pas d'effet, ce que l'on ne sait pas a priori) à un témoin, il y a des chances non négligeables pour qu'une ou deux "sortent du lot" par hasard. Bonferroni corrige cela.
Idée fausse et autres idées
"Une ANOVA doit précéder les comparaisons corrigées par Bonferroni".
En réalité, une ANOVA doit absolument précéder les comparaisons menées avec un test de Fisher PPDS (Plus Petite Différence Significative; "Fisher LSD" pour "Least Significant Difference" en anglais) qui est un test test "post-hoc" ou "a posteriori", mais pas la correction par Bonferroni qui est une procédure "a priori" basée sur un calcul de probabilités. Mais un grand nombre "d'experts" pour revues scientifiques l'ignorent.
Les tests de Tukey, Neuman-Keuls et Dunnett sont considérés comme tests a posteriori (et ne sont effectués qu'après une ANOVA préalable), mais d'après Zar (1999) cette ANOVA préalable ne se justifie pas en raison de la théorie sur laquelle ils sont basés...
Biblio
Zar JH. 1999. Biostatistical analysis. Fourth Ed. Prentice Hall, Upper Saddle River, New Jersey. pp663.
Retour aux articles de la catégorie Stats : choisir son test -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres