Un trait de lumière sur le t de Student
Résumé de la méthode 1
Dans la partie "La question que l'on se pose", nous avons vu que la question pertinente était : "Quelle est la probabilité pour obtenir par hasard la différence de moyenne que nous avons observée entre les deux groupes ?". Si cette probabilité est forte, on attribue cette différence à l'effet du hasard. Si elle est faible, on aura tendance à dire que cette différence est due à l'effet du traitement. Nous avons résolu le problème par une méthode "de ré-échantillonnage" proche de la méthode de Monte-Carlo. Telle que nous l'avons présentée, cette méthode nous a simplement servi à comprendre une étape. Elle n'est matériellement pas réalisable, car d'une part, on ne peut pas se permettre de mesurer la VD sur un nombre suffisant de sujets, et d'autre part il faudrait la refaire à chaque fois que l'on change de population ou de VD.
Résumé de la méthode 2
Nous avons alors eu une autre approche intuitive consistant à analyser les éléments qui étaient pris en compte lors d'une telle décision. Nous avions conclu que :
- Plus la différence de moyennes augmente, plus nous avons tendance à conclure que le traitement a un effet,
- Plus les variabilités augmentent, moins on a de facilité à prendre la décision,
- Plus l'effectif des échantillons augmente, plus on a de facilités à prendre la décision.
Les chapitres suivants nous ont permis de trouver des moyens de quantifier ces trois éléments.
Démystification du t de Student pour comparer deux moyennes
Tout semble montrer que Monsieur William Gosset (alias Student), en 1908, a copié notre raisonnement : il propose la formule :
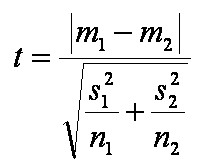
Nous voyons que :
- Plus la différence de moyennes (m1-m2) augmente, plus nous avons de facilité à conclure que le traitement a un effet, et… plus le "t" augmente,
- Plus les variabilités (s1 et s2) augmentent, moins on a de facilité à prendre la décision, et plus le t diminue,
- Plus l'effectif (n1 et n2) des échantillons augmente, plus on a de facilité à prendre la décision et plus le t augmente.
En d'autres termes, si t est élevé, on conclura avec assurance que le traitement a un effet, alors que s'il est faible on aura soit du mal à conclure, soit on dira que le traitement semble ne pas avoir d'effet.
A partir de quelle valeur le t est-il considéré comme "élevé" ?
Student (Gosset) a calculé, par des procédés mathématiques, la probabilité pour que le t dépasse certaines valeurs par hasard (si le traitement n'a, en réalité, pas d'effet), en fonction des effectifs des échantillons. L'intérêt du t de Student est qu'il peut s'appliquer à un nombre considérable d'échelle de données (contrairement à la méthode 1, il n'y a pas besoin de recalculer sa distribution pour chaque nouvelle population et pour chaque nouvelle VD).
En général, en biologie, si un résultat (une différence de moyenne entre un groupe traité et un groupe non traité) apparaît, et que ce résultat a moins de 5% de chances d'apparaître par hasard (si le traitement n'a pas d'effet réel), alors on considère que le résultat obtenu n'est pas dû au hasard mais au traitement.
Par exemple, si vous avez 2 groupes de 10 sujets. L'un des deux groupes reçoit une drogue qui pourrait avoir des effets (positifs ou négatifs) sur la mémoire. Ces sujets passent ensuite un test de mémoire, et on mesure les performances de chaque sujet. Enfin, on en fait la moyenne et on calcule le t de Student.
Student a calculé qu'il y avait 5% de chances que, si le traitement n'a en réalité pas d'effet, le t dépasse 2,10.
Ainsi, si le t que nous avons calculé dépasse 2,10, c'est qu'on a moins de 5% de chances d'obtenir ce résultat par hasard. On considérera donc que c'est le traitement qui a eu un effet. S'il est inférieur à 2,10, c'est que nous avons plus de 5% de chances de l'obtenir par hasard, et donc on ne pourra pas attribuer cette différence de moyenne à un effet du traitement avec une confiance suffisante.
Votre meilleur ami (qui est très honnête) joue au loto pour la première fois : il gagne 500000€! Vous vous dites : "Quelle chance !". Le lendemain, il rejoue : il re-gagne : 800000€! Vous vous dites : "Soit il triche, soit il a un don de voyance, mais ça ne peut plus être de la chance". C'est exactement la même logique avec le t de Student.
De même que dans la méthode 1, si le traitement n'a en réalité pas d'effet, le t que nous calculons a de fortes chances d'être proche de 0. Il a des chances très faibles d'être très éloigné de 0. C'est pour cela que la table des t de Student nous donne la valeur du t à partir de laquelle la probabilité est inférieure à 5%.
Mmmmh... Je sais pas si je suis très clair. Eventuellement, laissez un commentaire pour préciser ce qui n'est pas compris...
Page suivante : Hypothèses unilatérales et bilatérales
Page précédente : Erreur type
Retour au plan
Dans la partie "La question que l'on se pose", nous avons vu que la question pertinente était : "Quelle est la probabilité pour obtenir par hasard la différence de moyenne que nous avons observée entre les deux groupes ?". Si cette probabilité est forte, on attribue cette différence à l'effet du hasard. Si elle est faible, on aura tendance à dire que cette différence est due à l'effet du traitement. Nous avons résolu le problème par une méthode "de ré-échantillonnage" proche de la méthode de Monte-Carlo. Telle que nous l'avons présentée, cette méthode nous a simplement servi à comprendre une étape. Elle n'est matériellement pas réalisable, car d'une part, on ne peut pas se permettre de mesurer la VD sur un nombre suffisant de sujets, et d'autre part il faudrait la refaire à chaque fois que l'on change de population ou de VD.
Résumé de la méthode 2
Nous avons alors eu une autre approche intuitive consistant à analyser les éléments qui étaient pris en compte lors d'une telle décision. Nous avions conclu que :
- Plus la différence de moyennes augmente, plus nous avons tendance à conclure que le traitement a un effet,
- Plus les variabilités augmentent, moins on a de facilité à prendre la décision,
- Plus l'effectif des échantillons augmente, plus on a de facilités à prendre la décision.
Les chapitres suivants nous ont permis de trouver des moyens de quantifier ces trois éléments.
Démystification du t de Student pour comparer deux moyennes
Tout semble montrer que Monsieur William Gosset (alias Student), en 1908, a copié notre raisonnement : il propose la formule :
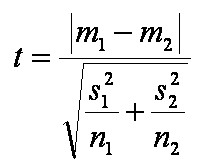
Nous voyons que :
- Plus la différence de moyennes (m1-m2) augmente, plus nous avons de facilité à conclure que le traitement a un effet, et… plus le "t" augmente,
- Plus les variabilités (s1 et s2) augmentent, moins on a de facilité à prendre la décision, et plus le t diminue,
- Plus l'effectif (n1 et n2) des échantillons augmente, plus on a de facilité à prendre la décision et plus le t augmente.
En d'autres termes, si t est élevé, on conclura avec assurance que le traitement a un effet, alors que s'il est faible on aura soit du mal à conclure, soit on dira que le traitement semble ne pas avoir d'effet.
A partir de quelle valeur le t est-il considéré comme "élevé" ?
Student (Gosset) a calculé, par des procédés mathématiques, la probabilité pour que le t dépasse certaines valeurs par hasard (si le traitement n'a, en réalité, pas d'effet), en fonction des effectifs des échantillons. L'intérêt du t de Student est qu'il peut s'appliquer à un nombre considérable d'échelle de données (contrairement à la méthode 1, il n'y a pas besoin de recalculer sa distribution pour chaque nouvelle population et pour chaque nouvelle VD).
En général, en biologie, si un résultat (une différence de moyenne entre un groupe traité et un groupe non traité) apparaît, et que ce résultat a moins de 5% de chances d'apparaître par hasard (si le traitement n'a pas d'effet réel), alors on considère que le résultat obtenu n'est pas dû au hasard mais au traitement.
Par exemple, si vous avez 2 groupes de 10 sujets. L'un des deux groupes reçoit une drogue qui pourrait avoir des effets (positifs ou négatifs) sur la mémoire. Ces sujets passent ensuite un test de mémoire, et on mesure les performances de chaque sujet. Enfin, on en fait la moyenne et on calcule le t de Student.
Student a calculé qu'il y avait 5% de chances que, si le traitement n'a en réalité pas d'effet, le t dépasse 2,10.
Ainsi, si le t que nous avons calculé dépasse 2,10, c'est qu'on a moins de 5% de chances d'obtenir ce résultat par hasard. On considérera donc que c'est le traitement qui a eu un effet. S'il est inférieur à 2,10, c'est que nous avons plus de 5% de chances de l'obtenir par hasard, et donc on ne pourra pas attribuer cette différence de moyenne à un effet du traitement avec une confiance suffisante.
Votre meilleur ami (qui est très honnête) joue au loto pour la première fois : il gagne 500000€! Vous vous dites : "Quelle chance !". Le lendemain, il rejoue : il re-gagne : 800000€! Vous vous dites : "Soit il triche, soit il a un don de voyance, mais ça ne peut plus être de la chance". C'est exactement la même logique avec le t de Student.
De même que dans la méthode 1, si le traitement n'a en réalité pas d'effet, le t que nous calculons a de fortes chances d'être proche de 0. Il a des chances très faibles d'être très éloigné de 0. C'est pour cela que la table des t de Student nous donne la valeur du t à partir de laquelle la probabilité est inférieure à 5%.
Mmmmh... Je sais pas si je suis très clair. Eventuellement, laissez un commentaire pour préciser ce qui n'est pas compris...
Page suivante : Hypothèses unilatérales et bilatérales
Page précédente : Erreur type
Retour au plan
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres