La moyenne des écarts à la moyenne
Le second à être proposé est la "moyenne des écarts à la moyenne". L'idée est de calculer :
- la moyenne des données du groupe,
- la différence entre chaque valeur et cette moyenne,
- la valeur absolue de chacune de ces différences (cette étape est en général oubliée par les étudiants mais il est facile de constater que la somme de ces différences sera nulle si on n'en prend pas la valeur absolue),
- la somme de toutes ces différences,
- diviser cette somme par le nombre d'individus.
La formule est la suivante :
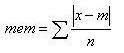
[avec x=valeur de chaque individu, m=moyenne de toutes ces valeurs, et n=nombre de valeurs dans l'échantillon]
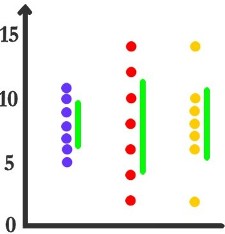
Sur le plan intuitif, cet indice est excellent. Il suffit d'observer sa représentation sur le graphique.
Hélas, ce n'est pas celui-là qui a été choisi par les mathématiciens.
Page suivante : La variance
Page précédente : Les extrêmes
Retour au plan
- la moyenne des données du groupe,
- la différence entre chaque valeur et cette moyenne,
- la valeur absolue de chacune de ces différences (cette étape est en général oubliée par les étudiants mais il est facile de constater que la somme de ces différences sera nulle si on n'en prend pas la valeur absolue),
- la somme de toutes ces différences,
- diviser cette somme par le nombre d'individus.
La formule est la suivante :
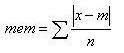
[avec x=valeur de chaque individu, m=moyenne de toutes ces valeurs, et n=nombre de valeurs dans l'échantillon]

Sur le plan intuitif, cet indice est excellent. Il suffit d'observer sa représentation sur le graphique.
Hélas, ce n'est pas celui-là qui a été choisi par les mathématiciens.
Page suivante : La variance
Page précédente : Les extrêmes
Retour au plan
A découvrir aussi
- Déroulement d'une recherche
- Opérationnalisation des VI en facteurs
- Variables dont il faut contrôler l'effet
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres