NeuropsychoJolly (roger)

Cette fiche a deux objectifs :
- d'un point de vue théorique, fixer, commencer une certaine formalisation, des résultats des expériences de Freeman, notamment en introduisant la notion de "chaos déterministe",
- d'un point de vue méthodologique, familiariser le lecteur avec les notions "d'attracteur d'activité", "d'espace d'état" étant donné que ces deux notions font appel à des cartes topographiques qui ressemblent (visuellement) aux cartes d'activité d'EEG, mais qui en sont totalement différentes dans leur signification.

Espace d'état : Si l'on résume les 64 dimensions en 2 dimensions, cela se traduit par un "nuage" de points sur un graphique à 2 dimensions. Ce graphique peut être appelé un "espace d'état", c'est-à-dire, un "espace" sur lequel peut être représenté chaque "état" du système, décrit par l'activité enregistrée par 64 électrodes.
Cette représentation en 2D est pratique pour visualiser les états pris par le système. Pour être plus rigoureux (mais moins pédagogique), il est également possible de travailler directement sur l'espace à 64 dimensions, qui sera également appelé "espace d'état". Les mathématiques sont juste un peu plus compliquées.

Nous avons vu que chaque (bulbe olfactif de) lapin était caractérisé par une "signature", ou carte de l'EEG, que l'on retrouve à chaque enregistrement, mais qui n'est jamais strictement identique.
L'association d'une odeur avec un renforcement crée une nouvelle signature propre à cette odeur pour ce lapin, qui est différente de celle de l'animal qui ne respire pas d'odeur particulière ou une odeur inconnue.
Après apprentissage de 3 odeurs, on obtient le graphique 2D suivant (déjà vu précédemment) et l'on sait qu'il faut y voir un résumé du même graphique en 64D.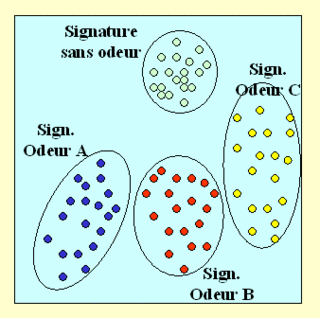



Attracteur d'activité : Les nuages 2D (ou hypernuages 64D) sont donc des zones de l'espace d'état qui sont "préférées" par le système. On dit que ces zones sont des "attracteurs" d'activité.
Attracteur implique attraction implique déplacement.


Représentation d'un attracteur dans un espace d'état
C'est ici que reviennent nos cartes topographiques dans un nouveau rôle.
Imaginons que notre graphique 2D ait des creux et des bosses (vallées, cratères, gouffres, montagnes).
Si l'on place une bille quelque part, au hasard sur ce graphique, la bille aura tendance à rouler pour aller se stabiliser dans un puits, ou continuer sa route dans une cuvette à fond plat, comme une boule dans un billard qui n'aurait pas de trou.
Ces puits et cuvettes à fond plat constituent des attracteurs pour la bille.
Avec cette analogie, un lapin qui a appris 3 odeurs mais qui n'en respire aucune en particulier, voit l'état de son système "localisé" à l'intérieur du nuage attracteur "signature sans odeur". Son état (ou le point le représentant) se "déplace" dans cette cuvette à fond plat que l'on appelle "bassin d'attraction".
La présentation soudaine de l'odeur B à ce lapin se traduit par un changement de bassin d'attraction : la bille va rouler dans le bassin B et s'y promener.
On peut donc dessiner des "trajectoires dans l'espace d'état", qui représentent l'évolution du système pendant un laps de temps donné. Cette trajectoire dépend des stimuli présents et des différents bassins existant.

Effectuer l'apprentissage d'une nouvelle odeur revient à "creuser" un nouveau bassin d'attraction sur la carte, tout en déplaçant tous ceux qui existent déjà.

A priori, l'emplacement du bassin d'attraction de la nouvelle odeur et les nouveaux bassins d'attraction des odeurs déjà connues ne peuvent pas être prédit. Pourtant, on se doute que ces différents emplacements dépendent à la fois des caractéristiques du stimulus (quels sont les récepteurs stimulés par l'odeur) et par l'histoire du système (le "vécu" du cerveau).
Actuellement, connaissant le temps qu'il fait un jour donné, on est capable de prédire celui qu'il fera le lendemain. Pourtant, on est incapable de faire des prévisions météo fiables à 10 jours.
Etant donné l'aspect imprédictible, on parle de "chaos", mais comme on sait que l'état à un moment donné dépend des états passés, ce chaos est qualifié de "déterministe". De même, la formation ou la modification des espaces d'état dans le cerveau sont soumises au chaos déterministe.