Comment résumer 64 valeurs en 2 valeurs
L'opération est identique si l'on veut résumer 60 valeurs en 2 valeurs, ou 60 en 1, ou 2 en 1.
Sauf que c'est plus facile à expliquer si l'on veut résumer 2 valeurs en 1.
Nous avons 1 cerveau et 2 électrodes implantées.
On admet que l'électrode 1 est placée dans une structure qui active la structure de l'électrode 2.
Mais la structure 2 est également un peu activée par d'autres structures. Les ondes enregistrées sous 2 vont donc être en grande partie corrélées avec celles enregistrées sous 1, mais pas totalement à cause des autres structures.
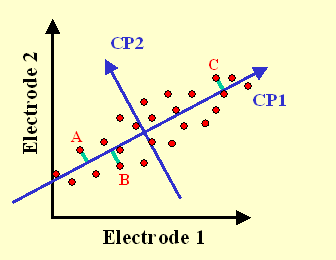
On peut donc calculer une droite qui passe au plus près de chaque point. Cette droite s'appelle la "première composante principale" (CP1).
Si on se situe sur un point et que l'on cherche à rejoindre la CP1 par le trajet le plus court, notre trajet est perpendiculaire à cette CP1.
Si cette CP1 a une échelle (une métrique), le point d'impact sur la CP1 peut être considéré comme une coordonnée. Cette coordonnée (unique) est le meilleur résumé que l'on puisse faire de nos deux valeurs initiales.
Dans un résumé de texte, on tente de donner le maximum d'information contenue dans le texte, avec moins de mots, mais on perd forcément un peu d'information.
De même, si on donne la coordonnée sur la CP1, on a le meilleur résumé possible des deux valeurs caractérisant ce point.
Si en plus, on donne la coordonnée sur l'axe perpendiculaire à la CP1 (cet axe est la CP2), on est capable de retrouver exactement les valeurs du point sous chaque électrode, mais ce n'est plus un résumé, c'est une reformulation.
La connaissance des coordonnées de A, B et C sur CP1 nous renseigne sur les "ressemblances" (ou proximités) entre ces trois points. Mais on peut également calculer directement la distance qui les sépare à partir des 2 valeurs qui caractérisent chacun des points.
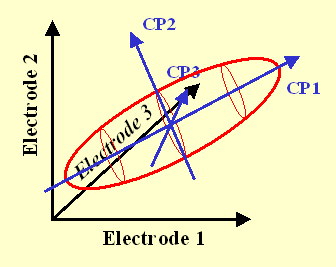
Avec trois électrodes, le nuage de points ressemblera à une dragée (en 3 dimensions).
On pourra calculer CP1 qui sera l'axe longitudinal de la dragée, CP2 qui sera l'axe transversal et CP3 (coupant par la face la plus étroite).
Le résumé sera CP1, ou [CP1 et CP2]. Avec CP1 et CP2, on peut tracer un graphique à 2 dimensions résumant les 3 initiales.
Mais on peut aussi, sans résumer calculer des distances entre des points dans un espace à 3 dimensions.
Avec 64 électrodes, on ne tracera pas d'hyperdragée dans un hyperespace à 64 dimensions mais on pourra quand même calculer CP1 et CP2 pour résumer les 64 enregistrements.
On pourra représenter par un point sur un graphique à 2 dimensions chaque ensemble de 64 enregistrements.
On peut également calculer des distances entre 2 points dans un hyperespace à 64 dimensions.
Sauf que c'est plus facile à expliquer si l'on veut résumer 2 valeurs en 1.
Nous avons 1 cerveau et 2 électrodes implantées.
On admet que l'électrode 1 est placée dans une structure qui active la structure de l'électrode 2.
Mais la structure 2 est également un peu activée par d'autres structures. Les ondes enregistrées sous 2 vont donc être en grande partie corrélées avec celles enregistrées sous 1, mais pas totalement à cause des autres structures.
On peut donc calculer une droite qui passe au plus près de chaque point. Cette droite s'appelle la "première composante principale" (CP1).
Si on se situe sur un point et que l'on cherche à rejoindre la CP1 par le trajet le plus court, notre trajet est perpendiculaire à cette CP1.
Si cette CP1 a une échelle (une métrique), le point d'impact sur la CP1 peut être considéré comme une coordonnée. Cette coordonnée (unique) est le meilleur résumé que l'on puisse faire de nos deux valeurs initiales.
Dans un résumé de texte, on tente de donner le maximum d'information contenue dans le texte, avec moins de mots, mais on perd forcément un peu d'information.
De même, si on donne la coordonnée sur la CP1, on a le meilleur résumé possible des deux valeurs caractérisant ce point.
Si en plus, on donne la coordonnée sur l'axe perpendiculaire à la CP1 (cet axe est la CP2), on est capable de retrouver exactement les valeurs du point sous chaque électrode, mais ce n'est plus un résumé, c'est une reformulation.
La connaissance des coordonnées de A, B et C sur CP1 nous renseigne sur les "ressemblances" (ou proximités) entre ces trois points. Mais on peut également calculer directement la distance qui les sépare à partir des 2 valeurs qui caractérisent chacun des points.

Avec trois électrodes, le nuage de points ressemblera à une dragée (en 3 dimensions).
On pourra calculer CP1 qui sera l'axe longitudinal de la dragée, CP2 qui sera l'axe transversal et CP3 (coupant par la face la plus étroite).
Le résumé sera CP1, ou [CP1 et CP2]. Avec CP1 et CP2, on peut tracer un graphique à 2 dimensions résumant les 3 initiales.
Mais on peut aussi, sans résumer calculer des distances entre des points dans un espace à 3 dimensions.

Avec 64 électrodes, on ne tracera pas d'hyperdragée dans un hyperespace à 64 dimensions mais on pourra quand même calculer CP1 et CP2 pour résumer les 64 enregistrements.
On pourra représenter par un point sur un graphique à 2 dimensions chaque ensemble de 64 enregistrements.
On peut également calculer des distances entre 2 points dans un hyperespace à 64 dimensions.
A découvrir aussi
- Le codage olfactif, son mystère, et l'entrée dans le cerveau
- Représentations distribuées : définition
- Aire V4 (18)
Retour aux articles de la catégorie Neurobiologie des processus cognitifs -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres