NeuropsychoJolly (roger)

MANOVA signifie "Multivariate Analysis of Variance", ou "Analyse de variance multivariée".

Ce type d'analyse peut vous aider à "détecter" un effet de facteur qui peut n'apparaître que si plusieurs variables dépendantes sont analysées simultanément.

Imaginons l'expérience suivante :
- un point de couleur apparaît sur un écran ayant un arrière plan uni.
- le sujet doit pointer ce point avec la flèche de la souris et cliquer dès qu'il se trouve dessus.
- dès que le clic est fait, le point disparaît et un autre apparaît ailleurs.
- le sujet a 1 minute pour cliquer sur un maximum de point, et le plus précisément possible

Les VDs :
- le temps moyen entre l'apparition du point et le clic,
- la distance entre le lieu précis du clic et le point.
Le FPS : l'âge, avec deux modalités : les 20-25 ans et les 85-90 ans

(l'expérience est purement imaginaire, et n'a pas été réalisée, les unités de temps et de distance sont arbitraire... mais l'exemple permet de comprendre les MANOVAs).

Je suis tenté de faire deux t de Student (1 par VD)

Je trouve :

********************
Two-sample t test on DISTANCE grouped by AGE$
 
Group         N          Mean          SD
Jeune        26        10.769        2.422
Vieux        26        11.962        2.720
 
Separate Variance t =       -1.669 df =   49.3    Prob =        0.101
Difference in Means =       -1.192   95.00% CI =     -2.627 to      0.243
 
Pooled Variance t =       -1.669 df =   50      Prob =        0.101
Difference in Means =       -1.192   95.00% CI =     -2.627 to      0.242
********************
Conclusion partielle : la différence entre les moyennes des "distances clic-point" des jeunes et des vieux n'est pas significative (t = 1.669; ddl = 50; p = 0.101), donc je ne peux pas conclure que les sujets âgés sont plus imprécis que les jeunes.

********************
Two-sample t test on TEMPS grouped by AGE$

Group    N    Mean    SD
Jeune               26        10.462        2.195
Vieux               26        11.462        2.420
 
Separate Variance t =       -1.560 df =   49.5    Prob =        0.125
Difference in Means =       -1.000   95.00% CI =     -2.287 to      0.287
 
Pooled Variance t =       -1.560 df =   50      Prob =        0.125
Difference in Means =       -1.000   95.00% CI =     -2.287 to      0.287
********************
Conclusion partielle : la différence entre les moyennes des "latences de clics" des jeunes et des vieux n'est pas significative (t = 1.560; ddl = 50; p = 0.125), donc je ne peux pas conclure que les sujets âgés ont des latences de clics plus grandes que les jeunes.

Conclusion générale : les jeunes ne se distinguent pas significativement des vieux sur cette tâche visuo-motrice au risque d'erreur alpha de 5%.

Qu'en est-il du résultat si on fait une MANOVA ?

Je trouve :

********************
Effects coding used for categorical variables in model.
 
Categorical values encountered during processing are:
AGE$ (2 levels)
   Jeune, Vieux
Number of cases processed: 52
Dependent variable means
 
                       ERREURS       TEMPS
                        11.365      10.962

[...Nombreuses lignes coupées ici...]

Test for effect called:     AGE$
 
[...Quelques lignes coupées ici...]
 
Univariate F Tests
 
     Effect         SS        df       MS              F              P
 
ERREURS            18.481     1       18.481          2.787          0.101
  Error           331.577    50        6.632
 
TEMPS              13.000     1       13.000          2.435          0.125
  Error           266.923    50        5.338
 
 
Multivariate Test Statistics
 
         Wilks' Lambda =       0.568
         F-Statistic =      18.670   df =   2,  49      Prob =       0.000
 
         Pillai Trace =       0.432
         F-Statistic =      18.670   df =   2,  49      Prob =       0.000
 
         Hotelling-Lawley Trace =       0.762
         F-Statistic =      18.670   df =   2,  49      Prob =       0.000
 
[...Quelques lignes coupées ici...]

********************
Dans le tableau "Univariate test", nous retrouvons les probabilités obtenues avec les t de Student. Cela signifie qu'aucun effet significatif du facteur "âge" n'est perceptible si on analyse les deux VDs de façon isolée.
Dans la partie 'Multivatiate Test Statistics", tout est significatif. Cela signifie que le facteur "âge" a un effet significatif sur les VD si on analyse cet effet simultanément sur les deux VDs.

Pour comprendre ce qui se passe, il suffit de regarder un graphique sur lequel on indique une VD en abscisse, l'autre en ordonnée et on "plotte" chaque individu en indiquant par un symbole à quel groupe il appartient... Le résultat est assez magique :



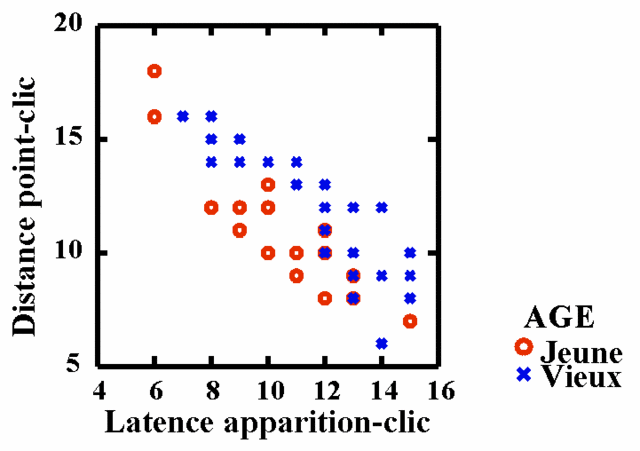
Sur le graphique, on s'aperçoit que les deux nuages de points sont relativement bien séparés.

Interprétation en français : les sujets qui "se précipitent" pour cliquer sont plus approximatifs (latence courte => grande distance). Cette "loi" semble vraie aussi bien pour les jeunes que pour les vieux, mais globalement, à latence égale, le jeune sera plus précis, et à précision égale, le jeune sera plus rapide. Si on ne regarde que les latence, la distinction n'apparaît pas, de même si on ne regarde que les distances.

Evidemment, l'interprétation est simple car nous n'avons que 2 VDs. On pourrait encore s'aider d'un graphique pour interpréter 3 VDs (espace à 3 dimensions); les choses se compliquent si l'on a 4 dimensions ou plus (hyper-espaces).
Les choses se compliquent également si l'on a plus de 2 modalités à notre facteur ou si l'on a plusieurs facteurs.

Que signifient les Wilks' Lambda, F-Statistic, Pillai Trace, Hotelling-Lawley Trace, Theta (non présent ici, présent seulement s'il y a plus de 2 modalités au facteur)?
Tous ces indicateurs disent la même chose : lorsque leur F est significatif, cela signifie qu'il doit y avoir une influence du facteur qui apparaît si on analyse plusieurs VD simultanément.
Le Wilks' Lambda est le plus utilisé mais présente des défauts...
La Pillai Trace serait plus robuste c'est-à-dire qu'elle est moins sensible aux "cas particuliers" de l'échantillonnage.
L'Hotelling-Lawley Trace doit également avoir ses qualités et ses défauts (je ne les connais pas).
Il existe également, le "Roy's maximum root" non donné par Systat.

En pratique, il faut en regarder plusieurs. Si ce qu'ils indiquent est concordant, cela signifie qu'il y a un ordre caché à identifier. Si les résultats ne sont pas concordants, c'est également qu'il doit se passer quelque chose, mais que les interprétations vont être "un peu" plus difficiles à tirer... (bon courage). Quoi qu'il en soit, plus votre plan expérimental sera simple (peu de facteurs, peu de modalités par facteur, peu de VDs) et plus vous avez de chances d'obtenir des résultats inter-indices cohérents et faciles à interpréter. (Sachez également que les VDs doivent être distribuées normalement, que les "sujets" doivent être indépendants, c'est-à-dire ne pas s'influencer mutuellement..., ce qui peut être la source de la discorde entre les indices).