NeuropsychoJolly (roger)

Le problème
Nous avons un facteur à deux modalités.
Deux variables quantitatives "mesurées" (par modalité).
On pourrait les appeler des VDs, mais la VD qui nous intéresse est le lien (la corrélation) entre ces 2 VDs (cf. exemple ci-dessous).
La question est de savoir si le facteur que l'on étudie influence la force de cette relation (mesurée par le coefficient de corrélation).
On peut donc mesurer un coefficient de corrélation entre les deux variables mesurées pour chacune des deux modalités et comparer ces deux coefficients de corrélations (chercher si leur différence est significative).

Procédure
1) On calcule les deux coefficients de corrélation (r1 et r2)
2) On effectue une transformation de Fisher (aussi appelée "normalisation" ou "transformation de r en z") à ces deux coefficients de corrélation... on obtient z1 et z2
3) On calcule Z (majuscule) que l'on compare aux valeurs de la loi normale trouvées dans une table.
- Si Zcalculé<Ztable on ne peut pas rejeter l'hypothèse nulle que les coefficients de corrélation sont égaux donc on ne peut pas conclure que le facteur a un effet sur l'intensité de la relation entre les deux variables mesurées
- Si Zcalculé>=Ztable on rejette l'hypothèse nulle que les coefficients de corrélation sont égaux (au risque d'erreur alpha choisi) et on conclue que les deux coefficients de corrélation sont significativement différents au risque d'erreur alpha choisi, c'est-à-dire que l'on considère, au risque d'erreur alpha choisi, que le facteur a un effet sur l'intensité de la relation entre les deux variables mesurées.

Table des Z; hypothèses bilatérales (2) et unilatérales (1)
Risque d'erreur alpha (2)   0.100     0.050     0.020     0.010     0.050
Risque d'erreur alpha (1)   0.050     0.025     0.010     0.005     0.025
Valeur critique du Z              1.64       1.96       2.33       2.58       2.81

Calculs
1) Calcul des coefficients de corrélation

2) Transformation de Fisher

          z = 0.5 ln[(1+r)/(1-r)]

(ln = log néperien)

3) Calcul de Z


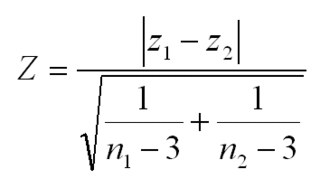
Exemple

Un groupe de souris jeunes et un groupe de souris âgées font un apprentissage.
On mesure l'activité cérébrale dans l'hippocampe et dans le cortex frontal.
On peut chercher à savoir si cet apprentissage entraîne une activité différente de ces deux structures en fonction de l'âge, mais ce n'est pas ce qui nous intéresse ici.
Ici, on veut savoir si l'apprentissage modifie la force de la relation (modifie la corrélation) entre ces deux structures.

Chez les jeunes, on trouve r=0.53
Chez les vieux, on trouve r=-0.40
Avec n = 16 dans chaque groupe

On fait ensuite la transformation de Fisher, ce qui donne
pour les jeunes, z=0.59
pour les vieux, z=-0.42

Et Z = 2.575

Dans une table de la loi normale, on trouve que le Z (de la table) = 1.96 (pour un risque d'erreur alpha de 0.05 et une hypothèse bilatérale).

2.575>1.96, donc on peut dire au risque d'erreur alpha de 0.05 que l'âge modifie la connectivité entre l'hippocampe et le cortex frontal à la suite de l'apprentissage qui a été effectué.