NeuropsychoJolly (roger)

Lorsqu'une personne est grande, on s'attend à ce que sa pointure soit élevée alors que si elle est petite, on s'attend à ce qu'elle est de petits pieds. Si c'est vrai, c'est qu'il existe une relation positive entre la taille de l'individu et celle de ses pieds.

Nous souhaitons disposer d'un indicateur qui mesure ce type de relation entre variables.

Rappelons nous la formule de l'estimation de la variance d'une population à partir d'un échantillon. Cette variance mesurait la variabilité des individus dans cette population.

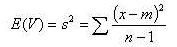
On aurait également pu écrire :

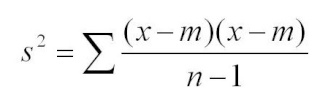
Si nous avons deux variables mesurées sur chacun des individus dont nous disposons, essayons de remplacer le deuxième "x-m" (avec m qui est la moyenne des x) par "y-m" (avec m qui est la mouyenne des y). s² était la variance; s_xy s'appellera la covariance. Ca nous donne :

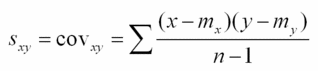
Testons cette formule dans les trois cas suivants :

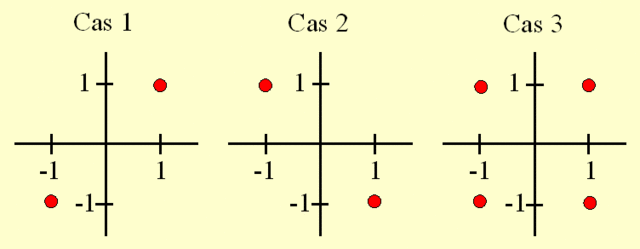
Cas 1 :

cov = ((1-0)(1-0)+(-1-0)(-1-0))/(2-1)

cov = (1+1)/1 = 2

Cas 2 :

cov = ((-1-0)(1-0)+(1-0)(-1-0))/(2-1)

cov = (-1+(-1))/1 = - 2

Cas 3 :

cov = ((1-0)(1-0)+(-1-0)(-1-0)+(-1-0)(1-0)+(1-0)(-1-0))/(4-1)

cov = (1+1+(-1)+(-1))/3 = 0

Nous avons trouvé un indicateur (la covariance) qui est positif lorsque la relation est positive, négatif lorsque la relation est négative, et nul lorsqu'il n'existe pas de relation.

C'est un grand progrès mais imaginons que dans l'exemple précédent, les mesures étaient faites en mètres. Quel serait le résultat si les mêmes mesures avaient été effectuées en centimètres (1m = 100cm)...

Cas 1 :

cov = ((100-0)(100-0)+(-100-0)(-100-0))/(2-1)

cov = (10000+10000)/1 = 20000

Cas 2 :

cov = ((-100-0)(100-0)+(100-0)(-100-0))/(2-1)

cov = (-10000+(-10000))/1 = - 20000

Cas 3 :

cov = ((100-0)(100-0)+(-100-0)(-100-0)+(-100-0)(100-0)+(100-0)(-100-0))/(4-1)

cov = (10000+10000+(-10000)+(-10000))/3 = 0

Nous constatons que si l'on change d'unité, le signe de la covariance nous renseigne toujours sur le sens de la relation. Une valeur nulle signale toujours une absence de relation. Par contre, la valeur elle même ne veut rien dire. La covariance est amétrique. Savoir qu'une covariance est égale à +325 nous signifie une relation positive, mais ne nous renseigne pas sur la force de la relation, tout dépend de l'unité.

Pour palier ce problème, les mathématiciens ont inventé la corrélation.

ATTENTION !!! Dans les formules ci-dessus, le dénominateur est n-1. On tente d'estimer la covariance des données de la population à partir d'un échantillon.

Dans d'autres manuels, vous trouverez n comme dénominateur. Les notations de la covariance de l'échantillon et de l'estimation de celle de la population ne sont en général pas distinguables. Ainsi, dans MsExcel, le dénominateur est n alors que dans Systat, c'est n-1... vous devez faire un calcul d'essai pour savoir quelle est la formule qui est utilisée par chaque nouveau logiciel utilisé... Super-pratique !