NeuropsychoJolly (roger)

Il représente l'amplitude des variations par rapport à la moyenne. Par exemple, la taille des êtres humains qui grandissent dans les appartements Parisiens n'est pas inférieure à la taille des être humains qui grandissent dans les steppes Mongoles. A l'inverse, des poissons rouges élevés dans un bocal ont une taille qui reste très réduite par rapport à des poissons rouges de la même espèce grandissant dans un étang. Le coefficient de variation de la population adulte humaine est donc très inférieur à celui de la population adulte des poissons rouges.



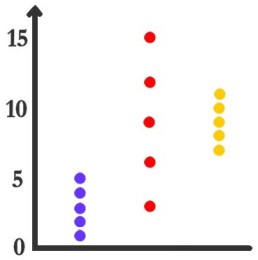
Sur le graphique, les groupes "bleu" et "orange" ont un écart type σ=1,41 alors que pour le groupe "rouge", σ=4,24. Par contre, les coefficients de variation des groupes "bleu" et "rouge" sont identiques : c.v.=47,1% (l'amplitude de la variation est de 47,1% par rapport à la moyenne), mais c.v.=15,7 pour le groupe "orange".

Le coefficient de variation peut être testé statistiquement mais n'a pas d'intérêt statistique. Son intérêt n'est que biologique.

Le coefficient de variation est noté c.v.

Selon les auteurs,



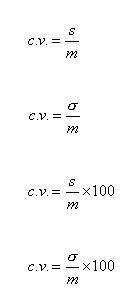
(les c.v. ont été ici calculés avec la formule 4 : on utilise σ car ce sont les échantillons qui nous intéressent, et les pourcentages pour que le lecteur se représente ce que signifie un c.v.).

Avec un peu de chance, l'auteur précise la formule qu'il utilise. Dans le cas contraire, c'est au lecteur de le deviner...

En règle générale on peut espérer que les première et troisième formules seront utilisées si on cherche à inférer le c.v. d'une population à partir d'un échantillon et les deux autres si c'est le c.v. de l'échantillon (ou si l'échantillon constitue la totalité de la population). On utilisera plutôt la première formule si on souhaite faire des tests statistiques sur ce paramètre (comparer les c.v. de deux populations à partir d'échantillons). Si l'on cherche à avoir un coefficient plus "intuitivement expressif" on choisira plutôt la troisième ou la quatrième car elles représentent des pourcentages.
Lorsqu'on lit un article et que la formule n'est pas indiquée, si le c.v. est nettement supérieur à 1, on a des chances qu'il s'agisse de la troisième ou quatrième formule et inversement si tous les c.v.cités sont inférieurs à 1, mais... rien n'est sûr !


Page suivante : Erreur type
Page précédente : Ecart type de la population
Retour au plan