Prendre un groupe comme son propre témoin
Nous voyons ici les niveau de stress d'individus en situation "placebo" et en situation "traité par anxiolytiques". Globalement, la moyenne en situation "traité" est inférieure à la moyenne en situation placebo, mais cette différence de moyenne n'est-elle pas due au hasard ?
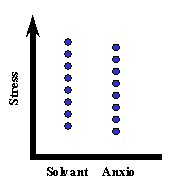
Admettons maintenant que les sujets en situation "placebo" et en situation "traité par anxiolytiques" sont les mêmes. On peut alors voir quel est le niveau de stress de chaque sujet en situation placebo et ce que devient celle-ci en situation anxiolytique. Sur les deux graphiques suivants on voit deux possibilités.
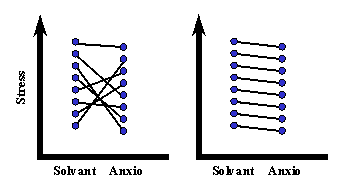
Le graphique de gauche montre une situation dans laquelle quelques sujets sont plus stressés lorsqu'ils ont pris l'anxiolytique. On a alors tendance à conclure que la différence entre les moyennes est probablement due à une variabilité naturelle des niveaux de stress au cours du temps. Eventuellement, on peut se dire que l'anxiolytique n'a pas le même effet sur tous les individus. On n'a alors pas tendance à attribuer cette différence de moyennes à l'effet de l'anxiolytique.
En langage un peu plus formel, on aura tendance à considérer que la différence de moyennes observée entre les groupes Solvant et Anxiolytique n'est pas due à l'effet de l'anxiolytique, mais aux variations naturelles des niveaux de stress des sujets.
Sur le graphique de droite, au contraire, on voit que chaque individu présente une diminution du niveau de stress en présence de l'anxiolytique. Celle-ci est faible, plus faible que la variabilité interindividuelle naturelle, mais très régulière. On aura alors tendance à attribuer la différence de moyenne à l'effet de l'anxiolytique.
Le test statistique correspondant (le t de Student pour échantillons appariés) est calqué exactement sur cette logique.
- On commence par calculer pour chaque individu, la différence entre les valeurs pour les deux modalités.
- On fait la moyenne de ces différences.
- Si certaines de ces différences sont positives et d'autres négatives (cas du graphique de gauche), alors ces valeurs auront tendance à s'annuler et la moyenne des différences sera proche de zéro.
- Si ces différences sont de façon homogène du même signe, alors, la valeur absolue de la moyenne de ces différences sera importante.
- Enfin, ce qui est moins visible sur les graphiques, si la variabilité de ces différences de moyennes est importante, nous aurons plus de mal à prendre une décision, et
- plus le nombre de sujets est important, plus nous aurons de facilité à prendre la décision.
Le t que nous devrons calculer a pour formule :
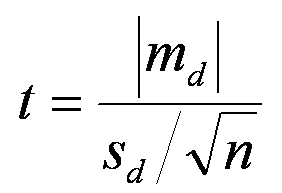
Avec md qui est la moyenne des différences, Sd, l'estimation de l'écart type des différences, et n, le nombre de sujets.
- Si ce "t" dépasse une valeur critique, cela signifiera que la variation que l'on observe entre les moyennes des modalités 1 et 2 de notre facteur a peu de chance d'être produite par les variations aléatoires naturelles des sujets.
Page suivante : Moralité : certains tests sont plus puissants que d'autres
Page précédente : Hypothèses unilatérales et bilatérales
Retour au plan

Admettons maintenant que les sujets en situation "placebo" et en situation "traité par anxiolytiques" sont les mêmes. On peut alors voir quel est le niveau de stress de chaque sujet en situation placebo et ce que devient celle-ci en situation anxiolytique. Sur les deux graphiques suivants on voit deux possibilités.

Le graphique de gauche montre une situation dans laquelle quelques sujets sont plus stressés lorsqu'ils ont pris l'anxiolytique. On a alors tendance à conclure que la différence entre les moyennes est probablement due à une variabilité naturelle des niveaux de stress au cours du temps. Eventuellement, on peut se dire que l'anxiolytique n'a pas le même effet sur tous les individus. On n'a alors pas tendance à attribuer cette différence de moyennes à l'effet de l'anxiolytique.
En langage un peu plus formel, on aura tendance à considérer que la différence de moyennes observée entre les groupes Solvant et Anxiolytique n'est pas due à l'effet de l'anxiolytique, mais aux variations naturelles des niveaux de stress des sujets.
Sur le graphique de droite, au contraire, on voit que chaque individu présente une diminution du niveau de stress en présence de l'anxiolytique. Celle-ci est faible, plus faible que la variabilité interindividuelle naturelle, mais très régulière. On aura alors tendance à attribuer la différence de moyenne à l'effet de l'anxiolytique.
Le test statistique correspondant (le t de Student pour échantillons appariés) est calqué exactement sur cette logique.
- On commence par calculer pour chaque individu, la différence entre les valeurs pour les deux modalités.
- On fait la moyenne de ces différences.
- Si certaines de ces différences sont positives et d'autres négatives (cas du graphique de gauche), alors ces valeurs auront tendance à s'annuler et la moyenne des différences sera proche de zéro.
- Si ces différences sont de façon homogène du même signe, alors, la valeur absolue de la moyenne de ces différences sera importante.
- Enfin, ce qui est moins visible sur les graphiques, si la variabilité de ces différences de moyennes est importante, nous aurons plus de mal à prendre une décision, et
- plus le nombre de sujets est important, plus nous aurons de facilité à prendre la décision.
Le t que nous devrons calculer a pour formule :
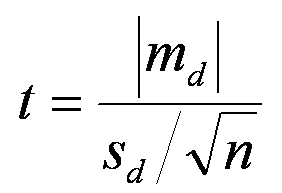
Avec md qui est la moyenne des différences, Sd, l'estimation de l'écart type des différences, et n, le nombre de sujets.
- Si ce "t" dépasse une valeur critique, cela signifiera que la variation que l'on observe entre les moyennes des modalités 1 et 2 de notre facteur a peu de chance d'être produite par les variations aléatoires naturelles des sujets.
Page suivante : Moralité : certains tests sont plus puissants que d'autres
Page précédente : Hypothèses unilatérales et bilatérales
Retour au plan
A découvrir aussi
- A quelles étapes les stats sont elles utiles ?
- Intérêt de cette typologie et de la connaissance des statuts
- Hypothèses, hypothèses fortes, hypothèses faibles
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres