Notion d'interaction statistique entre deux variables
Jusqu'à présent nous avons abordé uniquement des hypothèses qui mettaient en relation 1 FPS avec 1 VD.
Voyons maintenant le cas où nous voulons étudier simultanément les effets de 2 FPS.
Admettons que l'on ait montré un effet bénéfique du blocage de la dégradation de l'acétylcholine sur la mémoire chez les patients Alzheimer. Il s'agit d'un effet de récupération d'une fonction déficiente par rapport à une performance "normale".
Cette substance n'aurait-elle pas également des effets bénéfiques chez des sujets normaux. Il s'agit alors de tenter d'utiliser cette substance pour doper des individus non Alzheimer (veuillez excuser l'utilisation d'exemples aussi immoraux, je les désapprouve, mais ils sont extrêmement pratiques pour faire comprendre des notions telles que l'interaction statistique !!!).
Si nous avons au préalable montré que la substance améliorait les performances des sujets Alzheimer, il se peut qu'elle améliore également les sujets normaux, ou qu'elle n'ait d'effet que sur les sujets Alzheimer (une troisième possibilité peut formellement avoir lieu : qu'elle perturbe la mémoire des normaux, mais c'est peu probable). Si la substance améliore les performances dans les deux groupes, on dira qu'elle a un effet aussi bien sur les normaux que sur les Alzheimer. Si elle n'améliore que les Alzheimer, c'est qu'elle a un effet différent selon que le sujet est normal ou Alzheimer. Il s'agit d'une interaction statistique.
Formellement, on dit qu'il y a interaction lorsque :
"L'effet d'un FPS sur la VD n'est pas le même selon les modalités de l'autre FPS."
Lorsque je fais un cours de stats, tous les étudiants doivent apprendre par coeur cette "phrase magique". C'est d'ailleurs la seule chose à apprendre par coeur de tout le cours. Mais elle est extrèmement pratique pour interpréter correctement les résultats des mythiques "ANOVAs".
Nous voyons bien que l'effet du FPS "substance" sur la performance mnésique (VD) n'est pas le même selon les modalités ("normal" et "Alzheimer") du FPS "état cérébral".
Deuxième exemple immoral :
Etudiez l'effet des somnifères et de l'alcool :
- buvez de l'eau et avalez quelques bonbons : rien ne se passe
- buvez de l'eau et avalez quelques somnifères : vous allez dormir
- buvez de la vodka et avalez quelques bonbons : vous êtes ivre
- buvez de la vodka et avalez quelques somnifères : vous pensez que les conditions sont réunies pour faire de beaux rêves (sommeil + ivresse)... erreur : vous risquez le coma, voir la mort.
On constate qu'il n'y a pas addition des effets, mais phénomène d'interaction : l'effet du facteur "prise d'alcool" n'est pas le mêmes selon les modalités du facteur "autre substance absorbée".
Lorsque nous avons un plan d'expérience permettant d'étudier simultanément les effets de deux facteurs, on peut formuler des hypothèses portant sur trois ensembles de relations :
- 1 hypothèse sur l'effet du premier facteur
- 1 hypothèse sur l'effet du second facteur
- 1 hypothèse d'interaction entre les deux facteurs
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Je reformule...
(cette reformulation peut être utilisée pour mieux comprendre ce qu'est l'interaction, mais l'objectif est surtout de préparer le passage de sa compréhension intuitive à son utilisation en statistiques)
Admettons que :
le FPS1 est le traitement (modalités : "Placebo" et "Substance"),
le FPS2 est l'état de santé des patients ("Sains", "Pathologique"),
la VD est la "Performance".
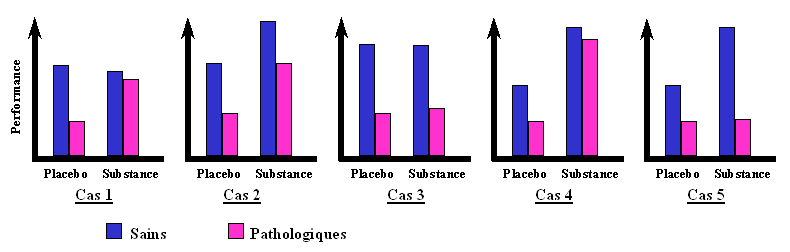
Voici ce que l'on a envie de dire :
Cas 1 : La substance a un effet uniquement sur les patients dont l'état est pathologique. Elle permet de pallier le déficit induit par la maladie.
Cas 2 : La substance a un effet positif quel que soit l'état des patients. Les sujets sains ont de meilleures performances que ceux qui sont atteints.
Cas 3 : Le traitement n'a pas d'effet. Les sujets sains ont de meilleures performances que ceux qui sont atteints.
Cas 4 : La substance permet pratiquement de pallier le déficit induit par la maladie. Elle a un effet positif chez tous les patients, mais plus prononcé chez les malades.
Cas 5 : La substance a un effet positif chez les sujets sains, qui ont de meilleures performances que ceux qui sont atteints. Elle n'a pas d'effet chez les sujets malades.
Voici ce que diront les statistiques :
En vert, c'est lorsque nos conclusions concordent avec ce que disent les statistiques.
En orange c'est lorsque nous ne sommes pas satisfaits par la réponse des statistiques.
Que ce soit pour le cas 1 FPS1, le cas 1 FPS2 ou le cas 5 FPS1, notre discordance avec les statistiques a deux origines :
- Nous voyons avant tout l'interaction qui est la seule à avoir du sens pour nous : le traitement n'a d'effet que sur un type de sujets, pas sur l'autre,
- Pour les statistiques, "effet global" ("main effect" en anglais) signifie "en moyenne", ou "globalement".
La même discordance serait apparue dans le cas 4 si les valeurs des groupes "sains" et "pathologiques" avaient été inversées dans la condition "substance".
Exemples d'interprétations "biologiques" :
Cas 1 : la substance a les propriétés de ce que l'on attend d'un médicament : elle ramène des sujets à un état "normal". Elle vient pallier un déficit.
Cas 2 : la substance est un dopant : elle améliore tout le monde.
Cas 3 : la substance est inefficace.
Cas 4 : la substance dope un système qui semble atteindre une limite chez les "sains".
Cas 5 : la substance dope un système, mais soit ce système est détruit dans la condition pathologique, soit la destruction d'un autre système chez les "pathologiques" tient lieu de facteur limitant de la performance.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Un cas plus simple d'interaction entre deux variables se présente lorsque l'un des deux facteurs est temporel. Par exemple : la séance d'apprentissage, le jour... Il implique donc une notion d'évolution.
Si c'est le FPS2 qui est temporel, la phrase magique devient :
"Le FPS1 provoque une différence d'évolution de la VD"
Il est pratique de la connaître par cœur, mais on peut s'en sortir si on ne connait que la première.
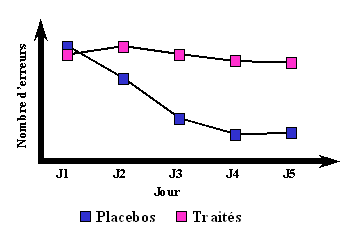
Nous voyons ici un exemple d'interaction avec un facteur temporel (décroissance du nombre d'erreurs au cours d'un apprentissage). L'autre facteur étudié serait l'effet d'une substance amnésiante.
Sur l'ensemble des 5 jours, il y a une interaction "jour x traitement". Il semble également y avoir un effet global du traitement (les placebos ont en moyenne moins d'erreurs que les traités), et un effet global du jour (en moyenne, le nombre d'erreurs décroît).
Dans ce type d'analyse, un effet du facteur traitement se traduit soit par une interaction, soit par un effet global du temps, soit par une interaction et un effet global du temps.
Nous pouvons noter que ce facteur a 5 modalités. On peut étudier des interactions entre facteurs qui ont plus de deux modalités même dans les cas où il n'y a aucun facteur temporel.
Si nous ne nous intéressons qu'à J1 et J2, il y a interaction, un très faible effet "traitement" et un très faible effet du jour. Mais si nous nous intéressons à J4 et J5, il n'y a pas d'interaction, il y a un fort effet du traitement, mais pas d'effet "jour". Ces deux analyses partielles montrent, par deux voies différentes, que la substance a un effet.
Page suivante : Interactions entre trois variables
Page précédente : Types d'hypothèses au cours d'une recherche
Retour au plan
Traduction statistique
Voyons maintenant le cas où nous voulons étudier simultanément les effets de 2 FPS.
Admettons que l'on ait montré un effet bénéfique du blocage de la dégradation de l'acétylcholine sur la mémoire chez les patients Alzheimer. Il s'agit d'un effet de récupération d'une fonction déficiente par rapport à une performance "normale".
Cette substance n'aurait-elle pas également des effets bénéfiques chez des sujets normaux. Il s'agit alors de tenter d'utiliser cette substance pour doper des individus non Alzheimer (veuillez excuser l'utilisation d'exemples aussi immoraux, je les désapprouve, mais ils sont extrêmement pratiques pour faire comprendre des notions telles que l'interaction statistique !!!).
Si nous avons au préalable montré que la substance améliorait les performances des sujets Alzheimer, il se peut qu'elle améliore également les sujets normaux, ou qu'elle n'ait d'effet que sur les sujets Alzheimer (une troisième possibilité peut formellement avoir lieu : qu'elle perturbe la mémoire des normaux, mais c'est peu probable). Si la substance améliore les performances dans les deux groupes, on dira qu'elle a un effet aussi bien sur les normaux que sur les Alzheimer. Si elle n'améliore que les Alzheimer, c'est qu'elle a un effet différent selon que le sujet est normal ou Alzheimer. Il s'agit d'une interaction statistique.
Formellement, on dit qu'il y a interaction lorsque :
"L'effet d'un FPS sur la VD n'est pas le même selon les modalités de l'autre FPS."
Lorsque je fais un cours de stats, tous les étudiants doivent apprendre par coeur cette "phrase magique". C'est d'ailleurs la seule chose à apprendre par coeur de tout le cours. Mais elle est extrèmement pratique pour interpréter correctement les résultats des mythiques "ANOVAs".
Nous voyons bien que l'effet du FPS "substance" sur la performance mnésique (VD) n'est pas le même selon les modalités ("normal" et "Alzheimer") du FPS "état cérébral".
Deuxième exemple immoral :
Etudiez l'effet des somnifères et de l'alcool :
- buvez de l'eau et avalez quelques bonbons : rien ne se passe
- buvez de l'eau et avalez quelques somnifères : vous allez dormir
- buvez de la vodka et avalez quelques bonbons : vous êtes ivre
- buvez de la vodka et avalez quelques somnifères : vous pensez que les conditions sont réunies pour faire de beaux rêves (sommeil + ivresse)... erreur : vous risquez le coma, voir la mort.
On constate qu'il n'y a pas addition des effets, mais phénomène d'interaction : l'effet du facteur "prise d'alcool" n'est pas le mêmes selon les modalités du facteur "autre substance absorbée".
Lorsque nous avons un plan d'expérience permettant d'étudier simultanément les effets de deux facteurs, on peut formuler des hypothèses portant sur trois ensembles de relations :
- 1 hypothèse sur l'effet du premier facteur
- 1 hypothèse sur l'effet du second facteur
- 1 hypothèse d'interaction entre les deux facteurs
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Je reformule...
(cette reformulation peut être utilisée pour mieux comprendre ce qu'est l'interaction, mais l'objectif est surtout de préparer le passage de sa compréhension intuitive à son utilisation en statistiques)
Admettons que :
le FPS1 est le traitement (modalités : "Placebo" et "Substance"),
le FPS2 est l'état de santé des patients ("Sains", "Pathologique"),
la VD est la "Performance".

Voici ce que l'on a envie de dire :
Cas 1 : La substance a un effet uniquement sur les patients dont l'état est pathologique. Elle permet de pallier le déficit induit par la maladie.
Cas 2 : La substance a un effet positif quel que soit l'état des patients. Les sujets sains ont de meilleures performances que ceux qui sont atteints.
Cas 3 : Le traitement n'a pas d'effet. Les sujets sains ont de meilleures performances que ceux qui sont atteints.
Cas 4 : La substance permet pratiquement de pallier le déficit induit par la maladie. Elle a un effet positif chez tous les patients, mais plus prononcé chez les malades.
Cas 5 : La substance a un effet positif chez les sujets sains, qui ont de meilleures performances que ceux qui sont atteints. Elle n'a pas d'effet chez les sujets malades.
Voici ce que diront les statistiques :
| | FPS1 (état de santé) | FPS2 (traitement) | FPS1 x FPS2 (interaction) |
| Cas 1 | Effet global (patho<sain) | Effet global (Subst>Placebo) | Il y a interaction |
| Cas 2 | Effet global (patho<sain) | Effet global (Subst>Placebo) | Pas d'interaction |
| Cas 3 | Effet global (patho<sain) | Pas d'effet global notable | Pas d'interaction |
| Cas 4 | Effet global (patho<sain) | Effet global (Subst>Placebo) | Il y a interaction |
| Cas 5 | Effet global (patho<sain) | Effet global (Subst>Placebo) | Il y a interaction |
En vert, c'est lorsque nos conclusions concordent avec ce que disent les statistiques.
En orange c'est lorsque nous ne sommes pas satisfaits par la réponse des statistiques.
Que ce soit pour le cas 1 FPS1, le cas 1 FPS2 ou le cas 5 FPS1, notre discordance avec les statistiques a deux origines :
- Nous voyons avant tout l'interaction qui est la seule à avoir du sens pour nous : le traitement n'a d'effet que sur un type de sujets, pas sur l'autre,
- Pour les statistiques, "effet global" ("main effect" en anglais) signifie "en moyenne", ou "globalement".
La même discordance serait apparue dans le cas 4 si les valeurs des groupes "sains" et "pathologiques" avaient été inversées dans la condition "substance".
Exemples d'interprétations "biologiques" :
Cas 1 : la substance a les propriétés de ce que l'on attend d'un médicament : elle ramène des sujets à un état "normal". Elle vient pallier un déficit.
Cas 2 : la substance est un dopant : elle améliore tout le monde.
Cas 3 : la substance est inefficace.
Cas 4 : la substance dope un système qui semble atteindre une limite chez les "sains".
Cas 5 : la substance dope un système, mais soit ce système est détruit dans la condition pathologique, soit la destruction d'un autre système chez les "pathologiques" tient lieu de facteur limitant de la performance.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Un cas plus simple d'interaction entre deux variables se présente lorsque l'un des deux facteurs est temporel. Par exemple : la séance d'apprentissage, le jour... Il implique donc une notion d'évolution.
Si c'est le FPS2 qui est temporel, la phrase magique devient :
"Le FPS1 provoque une différence d'évolution de la VD"
Il est pratique de la connaître par cœur, mais on peut s'en sortir si on ne connait que la première.

Nous voyons ici un exemple d'interaction avec un facteur temporel (décroissance du nombre d'erreurs au cours d'un apprentissage). L'autre facteur étudié serait l'effet d'une substance amnésiante.
Sur l'ensemble des 5 jours, il y a une interaction "jour x traitement". Il semble également y avoir un effet global du traitement (les placebos ont en moyenne moins d'erreurs que les traités), et un effet global du jour (en moyenne, le nombre d'erreurs décroît).
Dans ce type d'analyse, un effet du facteur traitement se traduit soit par une interaction, soit par un effet global du temps, soit par une interaction et un effet global du temps.
Nous pouvons noter que ce facteur a 5 modalités. On peut étudier des interactions entre facteurs qui ont plus de deux modalités même dans les cas où il n'y a aucun facteur temporel.
Si nous ne nous intéressons qu'à J1 et J2, il y a interaction, un très faible effet "traitement" et un très faible effet du jour. Mais si nous nous intéressons à J4 et J5, il n'y a pas d'interaction, il y a un fort effet du traitement, mais pas d'effet "jour". Ces deux analyses partielles montrent, par deux voies différentes, que la substance a un effet.
Page suivante : Interactions entre trois variables
Page précédente : Types d'hypothèses au cours d'une recherche
Retour au plan
Traduction statistique
A découvrir aussi
- Deuxième solution : les statistiques
- Intérêt de cette typologie et de la connaissance des statuts
- Analyse et rédaction des résultats d'une ANOVA à 1 facteur
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres