Moyenne d'un échantillon et moyenne de la population
Est-il nécessaire de rappeler comment on calcule une moyenne ? Derrière les trivialités de la question, il y a quand même des petites choses importantes.
J'ai eu 8 en maths, 2 en physique, 12 en histoire et 20 en philo, j'ai donc (8+2+12+20)/4=10,5 de moyenne. Sans commentaires.
Lorsque l'on veut calculer la moyenne des performances d'un groupe, c'est comme calculer la moyenne de la classe dans une discipline.
On additionne les notes de tous les élèves de la classe (ou de toutes les souris du groupe). Les élèves ou les souris sont appelés des "sujets". Ensuite on divise le résultat par le nombre de sujets.
Nous venons d'appliquer la formule :
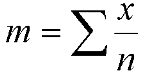
Sortons maintenant des trivialités :
Lorsque j'ai utilisé les notes de la totalité des élèves de la classe de terminale W du lycée Coubertin en 2008, on peut dire que j'ai travaillé sur la totalité de la "population des élèves de la classe de terminale W du lycée Coubertin de la promo de 2007". Si ce qui m'intéresse c'est d'avoir une idée de la moyenne de la totalité des élèves de terminale de France, je peux supposer qu'elle tournera autour de 10,5. 10,5 est une estimation faite à partir de la classe mesurée.
On se doute tout de suite que cette estimation n'est peut-être pas exacte en raison des caractéristiques du lycée (ce lycée pratique t'il une sélection à l'entrée, les parents paient-ils des cours particuliers...). Quoi qu'il en soit, si l'on ne connaît rien de plus sur ce lycée, la meilleure estimation que l'on puisse obtenir des élèves de France est 10,5. La seule chose qui nous gêne en disant cela, c'est ce que l'on peut appeler un problème de représentativité : le lycée était il représentatif des autres lycées de France ? Mais vu qu'on ne connaît rien de plus sur ce lycée, on ne peut pas faire mieux. Donc...
L'estimation de la moyenne de la population est égale à la moyenne de l'échantillon.
Pour les souris, c'est encore plus simple. Les populations sont standardisées, contrôlées... Lorsque l'on prend un groupe de souris, il est représentatif de la population des souris de laboratoire de cette lignée.
Comment améliorer cette estimation ?
Le seul moyen est d'augmenter le nombre de sujets sur lequel va porter l'estimation. On dit que l'on va augmenter la taille de l'échantillon.
Quel est le nombre minimum de sujets qu'il faut dans notre échantillon pour estimer cette moyenne de la population ?
15 ? 100 ?
100 c'est mieux que 15, mais 15 donne déjà une idée. Peut on faire moins ?
5 ? Ca marche aussi.
3 ? Ca marche encore.
2 ? Ca va pas être très précis mais on peut le faire.
1 ? Faut pas tomber sur un cas particulier mais on peut encore.
0 ? Ca n'est plus du tout possible
(On verra l'intérêt de ce baratin lors de l'estimation de la variance de la population à partir de l'échantillon.)
Page suivante : Indices de variabilité
Page précédente : Deuxième solution : les statistiques
Retour au plan
J'ai eu 8 en maths, 2 en physique, 12 en histoire et 20 en philo, j'ai donc (8+2+12+20)/4=10,5 de moyenne. Sans commentaires.
Lorsque l'on veut calculer la moyenne des performances d'un groupe, c'est comme calculer la moyenne de la classe dans une discipline.
On additionne les notes de tous les élèves de la classe (ou de toutes les souris du groupe). Les élèves ou les souris sont appelés des "sujets". Ensuite on divise le résultat par le nombre de sujets.
Nous venons d'appliquer la formule :
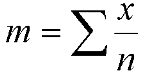
Sortons maintenant des trivialités :
Lorsque j'ai utilisé les notes de la totalité des élèves de la classe de terminale W du lycée Coubertin en 2008, on peut dire que j'ai travaillé sur la totalité de la "population des élèves de la classe de terminale W du lycée Coubertin de la promo de 2007". Si ce qui m'intéresse c'est d'avoir une idée de la moyenne de la totalité des élèves de terminale de France, je peux supposer qu'elle tournera autour de 10,5. 10,5 est une estimation faite à partir de la classe mesurée.
On se doute tout de suite que cette estimation n'est peut-être pas exacte en raison des caractéristiques du lycée (ce lycée pratique t'il une sélection à l'entrée, les parents paient-ils des cours particuliers...). Quoi qu'il en soit, si l'on ne connaît rien de plus sur ce lycée, la meilleure estimation que l'on puisse obtenir des élèves de France est 10,5. La seule chose qui nous gêne en disant cela, c'est ce que l'on peut appeler un problème de représentativité : le lycée était il représentatif des autres lycées de France ? Mais vu qu'on ne connaît rien de plus sur ce lycée, on ne peut pas faire mieux. Donc...
L'estimation de la moyenne de la population est égale à la moyenne de l'échantillon.
Pour les souris, c'est encore plus simple. Les populations sont standardisées, contrôlées... Lorsque l'on prend un groupe de souris, il est représentatif de la population des souris de laboratoire de cette lignée.
Comment améliorer cette estimation ?
Le seul moyen est d'augmenter le nombre de sujets sur lequel va porter l'estimation. On dit que l'on va augmenter la taille de l'échantillon.
Quel est le nombre minimum de sujets qu'il faut dans notre échantillon pour estimer cette moyenne de la population ?
15 ? 100 ?
100 c'est mieux que 15, mais 15 donne déjà une idée. Peut on faire moins ?
5 ? Ca marche aussi.
3 ? Ca marche encore.
2 ? Ca va pas être très précis mais on peut le faire.
1 ? Faut pas tomber sur un cas particulier mais on peut encore.
0 ? Ca n'est plus du tout possible
(On verra l'intérêt de ce baratin lors de l'estimation de la variance de la population à partir de l'échantillon.)
Page suivante : Indices de variabilité
Page précédente : Deuxième solution : les statistiques
Retour au plan
A découvrir aussi
- L'écart type
- Types d'hypothèses au cours d'une recherche
- Moralité : certains tests sont plus puissants que d'autres
Retour aux articles de la catégorie Méthodo et stats : comprendre -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres