Le t de Student pour échantillons appariés
Nous avons mesuré une VD à deux reprises sur un même groupe d'individus, mais dans deux conditions différentes. Nous avons vu la logique de ce test dans le chapitre "Prendre un groupe comme son propre témoin". En résumé, la logique du test consiste à comparer les deux mesures de chaque individu et à voir si la variation d'une condition à l'autre a toujours lieu dans le même sens. En langage mathématique, pour chaque individu, on fait la différence "mesure 2 - mesure 1" et on regarde si celle-ci a toujours le même signe. En d'autres termes, on ne travaille pas sur une différence de moyennes (comme c'est le cas lorsque les échantillons sont indépendants) mais sur une moyenne de différences
En théorie, la distribution de ces différences doit être normale. En pratique (c'est très mal) on le vérifie plutôt rarement. Nous savons si nous avons formulé une hypothèse forte ou faible.
Pour chaque individu, je donne le numéro de l'individu suivi de ses valeurs en condition 1 et 2.
i1(3, 6); i2(5, 7); i3(5, 9); i4(6, 9); i5(6, 9): i6(8, 10); i7(10, 12)
(Notez que les valeurs sont volontairement les mêmes que pour le chapitre t de Student pour échantillons indépendants afin de pouvoir comparer l'efficacité des tests).
___________________________
Utilisation d'un logiciel (Systat)
Les résultats ont été introduits dans le logiciel comme indiqué dans la rubrique "Logiciels" (1 sujet par ligne, 1 seul).
*************************************
Paired samples t test on CONDITION1 vs CONDITION2 with 7 cases
Mean CONDITION1 = 6.143
Mean CONDITION2 = 8.857
Mean Difference = -2.714 95.00% CI = -3.413 to -2.015
SD Difference = 0.756 t = -9.500
df = 6 Prob = 0.000
*************************************
L'hypothèse est-elle forte ou faible ?
Cas de l'hypothèse faible : le risque d'erreur alpha (risque que si le facteur n'a pas d'effet, on trouve un tel résultat à cause du hasard des fluctuations de la VD) est 0,000 (c'est-à-dire qu'il est inférieur à 0,001 ou inférieur à 1 pour 1000). On considère que c'est significatif car c'est inférieur à 5%. On peut conclure au risque d'erreur alpha de 0,001 que le traitement appliqué en condition 2 augmente la valeur de la VD par rapport à la condition 1.
Cas de l'hypothèse forte "le traitement appliqué en condition 2 augmente la valeur de la VD par rapport à la condition 1" : je constate que 6.143<8.857. Nous avons formulé une hypothèse unilatérale, donc on divise la probabilité trouvée (0.000) par 2, ce qui na pas de conséquences ici. Le risque d'obtenir une telle différence par hasard est donc inférieur à 1 pour 1000. Je peux conclure, au risque d'erreur alpha de 1 pour 1000 que le traitement appliqué en condition 2 augmente la valeur de la VD par rapport à la condition 1.
Cas de l'hypothèse forte "le traitement appliqué en condition 2 diminue la valeur de la VD par rapport à la condition 1" : je constate que c'est le contraire qui se produit (6.143<8.857). L'analyse s'arrète ici car l'hypothèse est unilatérale, je ne peux pas dire que le traitement reçu en condition 2 diminue la valeur de la VD par rapport à la condition 1... il faut comprendre ce qui a pu se passer pendant l'expérience, revoir la théorie, formuler de nouvelles hypothèses, refaire une expérience...
___________________________
Version "fait à la main"
Pour chaque individu, je calcule la différence entre sa VD en condition 1 et en condition 2 (toujours dans le même sens; on ne fait pas C1 - C2 pour un individu puis C2 - C1 pour un autre).
Je calcule md (la moyenne de ces différences) et E(Vd), c'est-à-dire l'estimation de la variance de ces différences pour la population.
Je connais n (le nombre d'individus).
md = 2,714; sd = 0,756; n = 7
Je calcule :
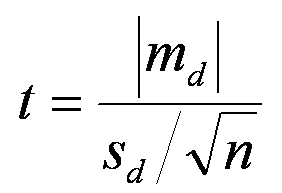
Je trouve : t = 9,5
Degrés de liberté : ddl = nu = n - 1= 6
Nous sommes maintenant muni du t calculé et du degré de liberté. On choisit alors un seuil de signification (en général 0.05 ou 0.01), et on va chercher dans une table des t de Student la valeur limite correspondante au seuil et au ddl. Cette valeur limite est celle à partir de laquelle le hasard a peu de chance de donner une valeur.
Dans le cas d'une hypothèse faible, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi.
Dans le cas d'une hypothèse forte et que la différence entre les moyennes va dans le sens de celle prédite par l'hypothèse, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi multiplié par 2.
Si le seuil choisi est 0.05, on regardera la colonne 0.10.
Si on ne dispose pas d'une table de t de Student, on peut trouver ces valeurs avec un tableur (type Excel et probablement OpenCalc). On fait :
Insérer/fonction/LOI.STUDENT.INVERSE qui demande le seuil et le ddl
ou on écrit dans une cellule :
=LOI.STUDENT.INVERSE(seuil;ddl)
Par exemple : "=LOI.STUDENT.INVERSE(0.05;6)" donne 2,447.
Si nous testons une hypothèse unilatérale (forte), on entrera
"=LOI.STUDENT.INVERSE(0.10;6)" qui donnera 1,943
On peut maintenant comparer le t calculé au t de la table :
Si le t calculé est supérieur à celui de la table (il dépasse la limite) le résultat a donc peu de chances d'être dû au hasard, on considère donc l'influence du traitement comme significative au seuil choisi.
Si le t calculé est inférieur à celui de la table, le résultat obtenu a pu être obtenu par hasard, et donc on ne peut pas considérer au seuil de confiance choisi que l'effet observé est dû au facteur étudié.
En théorie, la distribution de ces différences doit être normale. En pratique (c'est très mal) on le vérifie plutôt rarement. Nous savons si nous avons formulé une hypothèse forte ou faible.
Pour chaque individu, je donne le numéro de l'individu suivi de ses valeurs en condition 1 et 2.
i1(3, 6); i2(5, 7); i3(5, 9); i4(6, 9); i5(6, 9): i6(8, 10); i7(10, 12)
(Notez que les valeurs sont volontairement les mêmes que pour le chapitre t de Student pour échantillons indépendants afin de pouvoir comparer l'efficacité des tests).
___________________________
Utilisation d'un logiciel (Systat)
Les résultats ont été introduits dans le logiciel comme indiqué dans la rubrique "Logiciels" (1 sujet par ligne, 1 seul).
*************************************
Paired samples t test on CONDITION1 vs CONDITION2 with 7 cases
Mean CONDITION1 = 6.143
Mean CONDITION2 = 8.857
Mean Difference = -2.714 95.00% CI = -3.413 to -2.015
SD Difference = 0.756 t = -9.500
df = 6 Prob = 0.000
*************************************
L'hypothèse est-elle forte ou faible ?
Cas de l'hypothèse faible : le risque d'erreur alpha (risque que si le facteur n'a pas d'effet, on trouve un tel résultat à cause du hasard des fluctuations de la VD) est 0,000 (c'est-à-dire qu'il est inférieur à 0,001 ou inférieur à 1 pour 1000). On considère que c'est significatif car c'est inférieur à 5%. On peut conclure au risque d'erreur alpha de 0,001 que le traitement appliqué en condition 2 augmente la valeur de la VD par rapport à la condition 1.
Cas de l'hypothèse forte "le traitement appliqué en condition 2 augmente la valeur de la VD par rapport à la condition 1" : je constate que 6.143<8.857. Nous avons formulé une hypothèse unilatérale, donc on divise la probabilité trouvée (0.000) par 2, ce qui na pas de conséquences ici. Le risque d'obtenir une telle différence par hasard est donc inférieur à 1 pour 1000. Je peux conclure, au risque d'erreur alpha de 1 pour 1000 que le traitement appliqué en condition 2 augmente la valeur de la VD par rapport à la condition 1.
Cas de l'hypothèse forte "le traitement appliqué en condition 2 diminue la valeur de la VD par rapport à la condition 1" : je constate que c'est le contraire qui se produit (6.143<8.857). L'analyse s'arrète ici car l'hypothèse est unilatérale, je ne peux pas dire que le traitement reçu en condition 2 diminue la valeur de la VD par rapport à la condition 1... il faut comprendre ce qui a pu se passer pendant l'expérience, revoir la théorie, formuler de nouvelles hypothèses, refaire une expérience...
___________________________
Version "fait à la main"
Pour chaque individu, je calcule la différence entre sa VD en condition 1 et en condition 2 (toujours dans le même sens; on ne fait pas C1 - C2 pour un individu puis C2 - C1 pour un autre).
Je calcule md (la moyenne de ces différences) et E(Vd), c'est-à-dire l'estimation de la variance de ces différences pour la population.
Je connais n (le nombre d'individus).
md = 2,714; sd = 0,756; n = 7
Je calcule :
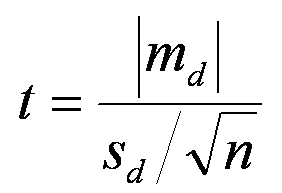
Je trouve : t = 9,5
Degrés de liberté : ddl = nu = n - 1= 6
Nous sommes maintenant muni du t calculé et du degré de liberté. On choisit alors un seuil de signification (en général 0.05 ou 0.01), et on va chercher dans une table des t de Student la valeur limite correspondante au seuil et au ddl. Cette valeur limite est celle à partir de laquelle le hasard a peu de chance de donner une valeur.
Dans le cas d'une hypothèse faible, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi.
Dans le cas d'une hypothèse forte et que la différence entre les moyennes va dans le sens de celle prédite par l'hypothèse, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi multiplié par 2.
Si le seuil choisi est 0.05, on regardera la colonne 0.10.
Si on ne dispose pas d'une table de t de Student, on peut trouver ces valeurs avec un tableur (type Excel et probablement OpenCalc). On fait :
Insérer/fonction/LOI.STUDENT.INVERSE qui demande le seuil et le ddl
ou on écrit dans une cellule :
=LOI.STUDENT.INVERSE(seuil;ddl)
Par exemple : "=LOI.STUDENT.INVERSE(0.05;6)" donne 2,447.
Si nous testons une hypothèse unilatérale (forte), on entrera
"=LOI.STUDENT.INVERSE(0.10;6)" qui donnera 1,943
On peut maintenant comparer le t calculé au t de la table :
Si le t calculé est supérieur à celui de la table (il dépasse la limite) le résultat a donc peu de chances d'être dû au hasard, on considère donc l'influence du traitement comme significative au seuil choisi.
Si le t calculé est inférieur à celui de la table, le résultat obtenu a pu être obtenu par hasard, et donc on ne peut pas considérer au seuil de confiance choisi que l'effet observé est dû au facteur étudié.
A découvrir aussi
Retour aux articles de la catégorie Stats : choisir son test -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres