Estimateurs "quadratique" et "robuste" de variabilité
Un étudiant m'a demandé pourquoi le statisticien avait choisi la variance pour estimateur de variabilité (estimateur quadratique) plutôt que la moyenne des écarts à la moyenne (estimateur robuste, intuitivement beaucoup plus naturel)...
Variance :
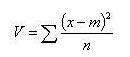
Moyenne des écarts à la moyenne :
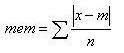
La question est posée en version longue sur Futura-Sciences. La réponse est loin d'être évidente.
Comme argument, on trouve :
- un estimateur quadratique permet de donner plus de poids aux valeurs extrèmes
- un estimateur quadratique aurait des propriétés mathématiques utiles qu'un estimateur non quadratique ne possèderait pas. En particulier que la variabilité de la somme de deux variables est la somme des variabilités de chacune (mais je n'ai pas vérifié que cette propriété ne s'applique pas à l'estimateur robuste).
... mais le premier argument est également utilisé pour dire que l'estimateur robuste est meilleur car il est moins sensible aux valeurs aberrantes...
De façon assez curieuse, l'écart type semble avoir été proposé avant la variance. Il aurait été inspiré de la méthode de calcul des barycentres.
Au moment où la question m'a été posée, j'avais l'impression que le sujet m'était famillier sans savoir pourquoi. En fait, nous nous étions déjà posé ce type de question avec Aurélie Boucard lorsque nous voulions comparer des matrices de corrélations (trouver une valeur unique permettant d'exprimer la différence entre deux tableaux de résultats). La variance ressemble à une distance Euclidienne, la moyenne des écarts à la moyenne ressemble à une différence. N'ayant pas pu trancher lequel des seux estimateurs était le meilleur, nous avions travaillé sur les deux simultanément.
Références
Origines de la variance - Futura-Sciences
Variance (statistiques et probabilités) - Wikipedia
De Moivre A (1718) The Doctrine of Chance.
Boucard et al. 2007. Reliability and validity of structural equation modeling applied to neuroimaging data: A simulation study. Journal of Neuroscience Methods 166 (2), 278-292.
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 76 autres membres