NeuropsychoJolly (roger)

L'analyse de variance (ou ANOVA pour ANalysis Of VAriance) à 1 facteur est utile lorsque l'on étudie l'effet d'un facteur à plus de 2 modalités. Elle peut également être utilisée lorsque l'on n'a que 2 modalités, mais elle devient alors redondante avec le t de Student.

Par exemple, j'étudie l'effet d'une substance. J'ai un groupe recevant le solvant et les trois autres groupes reçoivent respectivement trois concentrations différentes de cette substance. Ce qui me fait 1 facteur (substance) et 4 modalités : 1 solvant + 3 doses.

Nous avons vu que la "formule" du t de Student (cf. paragraphe en bleu) reflétait directement notre facilité à prendre une décision concernant le fait qu'une différence entre deux moyennes était due au facteur étudié ou pouvait être due au hasard (voir aussi "2^ème solution : les statistiques" pour les schémas explicatifs et le paragraphe en bleu).

La question statistique était alors : "quelle est la probabilité pour que la valeur du t soit aussi élevée que celle que j'observe si le facteur n'a pas d'effet réel ?". En d'autres termes : "quelle est la probabilité pour que la valeur du t soit aussi élevée si la différence que j'observe entre les moyennes des deux groupes est due au hasard ?".

La logique de l'ANOVA est moins intuitive mais très facilement compréhensible.

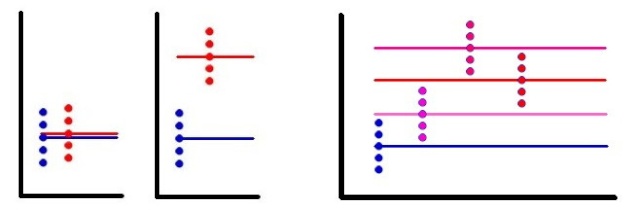
Sur ce premier schéma, on voit que si un facteur a un effet (graphique central par rapport au graphique de gauche où le facteur n'a pas d'effet), celà se traduit surtout par une différence entre les moyennes des deux groupes. Mais celà se traduit aussi par une augmentation de la variabilité des moyennes des deux groupes.

Si l'on regarde le graphique de droite, on observe une forte variabilité des moyennes des 4 groupes et on devine que celle-ci (variabilité) aurait été proche de 0 si le facteur n'avait pas eu d'effet. Si l'on veut traduire cette phrase en termes de différences de moyennes, c'est beaucoup plus compliqué : "les moyennes sont différentes entre elles", mais si 2 moyennes sont identiques et que les deux autres sont différentes, faut-il dire : "les moyennes sont différentes entre elles sauf...". Alors que si l'on parle en termes de variabilités des moyennes, il n'y a pas besoin de modifier son affirmation.

Si l'on regarde le deuxième schéma dans lequel le facteur n'a pas d'effet sur la moyenne, on constate que la variabilité des moyennes des groupes, dépend aussi de la variabilité des individus dans chaque groupe.

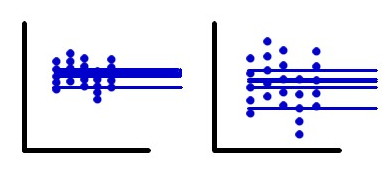
Le principe de l'analyse de variance est de calculer la probabilité d'obtenir une telle variabilité des moyennes, selon la variabilité des individus dans les groupes.

On calcule donc :

- la moyenne des variabilités des individus à l'intérieur de chaque groupe,

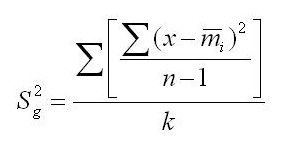
avec k=nombre de groupes; n=nombre d'individus par groupe, x=valeur de chaque individu

Pas clair ???
Σ(x-m)²/(n-1) c'est la variabilité des individus dans 1 groupe donné ou plus exactement l'estimation de la variabilité de la populations dont ce groupe est extrait (estimation de la variance = E(V))

On fait ça pour chaque groupe, puis pour faire la moyenne de toutes ces variabilités, on aditionne (premier Σ de l'équation) ces variabilités et on divise  cette somme par le nombre de groupes (k).

- la variabilité des moyennes

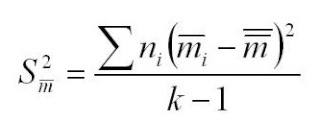
avec

= moyenne de chaque groupe; 

= moyenne des moyennes des groupes = M

Pas clair ???

C'est normal ! il ne s'agit pas exactement de la variance des moyennes autour de la moyenne générale sinon, ça donnerait :  Σ(m-M)²/(k-1) et non  Σn(m-M)²/(k-1). Il s'agit en fait d'une variance pondérée par l'effectif de chaque groupe : on donne plus de poids aux groupes qui ont plus de sujets.

- enfin, le rapport entre les deux, puis ce rapport permet de trouver la probabilité d'obtenir un tel rapport "par hasard" si le facteur n'a pas d'effet (grâce à une table de valeurs limites théoriques).

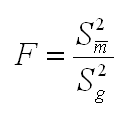
Dans les bouquins de stats, on trouvera plutôt des formules "simplifiées" (pour le calcul à la main) mais difficilement compréhensibles.