Le t de Student pour échantillons indépendants
A ce stade, nous avons mesuré une VD sur deux groupes d'individus différents. Celle-ci est distribuée de façon approximativement normale. Nous savons si nous avons formulé une hypothèse forte ou faible, si les variances sont à peu près égales...
Groupe 1 : 3, 5, 5, 6, 6, 8, 10
Groupe 2 : 6, 7, 9, 9, 9, 10, 12
___________________________
Utilisation d'un logiciel (Systat)
Les résultats ont été introduits dans le logiciel comme indiqué dans la rubrique "Logiciels".
*************************************
Group N Mean SD
G1 7 6.143 2.268
G2 7 8.857 1.952
Separate Variance t = -2.400 df = 11.7 Prob = 0.034
Difference in Means = -2.714 95.00% CI = -5.184 to -0.244
Pooled Variance t = -2.400 df = 12 Prob = 0.034
Difference in Means = -2.714 95.00% CI = -5.178 to -0.250
*************************************
Nous voyons qu'il y a 2 résultats : 1 avec Separate Variance, et l'autre avec Pooled
Les variances étaient elles différentes ?
(Normalement...) Nous avons fait le test de Snedecor pour savoir si l'on peut considérer les variances comme égales ou si elles diffèrent trop (test significatif).
Si les variances sont considérées comme identiques, on lira "Pooled". Sinon, on lira "Separate". Car si elles sont trop différentes, on doit corriger le degré de liberté. C'est la raison pour laquelle nous avons df=11.7 (cas corrigé) dans un cas et df=12 dans l'autre (df = degree of freedom = degré de liberté = ddl = nu = ...).
(En réalité...) Nous n'avons pas fait le test de Snedecor. Si le df de Separate est très différent de celui de Pooled, on prendra celui de separate (simplement car le logiciel apporte la correction juste nécessaire dans Separate avec la formule de Welsch et que lorsque les variances sont identiques, cette correction est nulle).
Si on constate que la probabilité est la même (ici 0.034), c'est qu'il est inutile de prendre la version "Separate".
L'hypothèse est elle forte ou faible ?
Cas de l'hypothèse faible : le risque d'erreur alpha (risque que si le facteur n'a pas d'effet, on trouve une telle différence de moyenne à cause du hasard de l'échantillonnage) est 0.034 (3,4%). On considère que c'est significatif car c'est inférieur à 5% (une telle différence n'a que 3,4% de chance de se produire si le facteur n'a en réalité pas d'effet, donc je l'attribue à l'effet du facteur). On peut conclure au risque d'erreur alpha de 3.4% que le traitement appliqué à G2 augmente la valeur de sa VD par rapport à G1.
Cas de l'hypothèse forte MeanG1>MeanG2 : je constate que c'est le contraire qui se produit (6.143<8.857). L'analyse s'arrête ici car l'hypothèse est unilatérale, je ne peux pas dire que le traitement reçu par G1 augmente la valeur de sa VD par rapport à G2... il faut comprendre ce qui a pu se passer pendant l'expérience, revoir la théorie, formuler de nouvelles hypothèses, refaire une expérience...
Cas de l'hypothèse forte MeanG1<MeanG2 : je constate que 6.143<8.857 et que les chances d'obtenir une telle différence par hasard est de 1,7%... (0.034/2 = 0.017, car l'hypothèse est unilatérale).
Je peux conclure, au risque d'erreur alpha de 1,7% que le traitement appliqué à G2 augmente la valeur de sa VD par rapport à G1.
___________________________
Version "fait à la main"
Je calcule m1, m2, E(V1), E(V2), je connais n1 et n2
m1 = 6.143; m2 = 8.857; E(V1) = 5.14; E(V2) = 3.81
Je calcule :
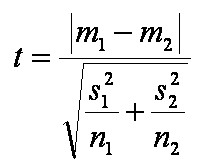
Je trouve : t = 2,4
Degrés de liberté :
Si le test de Snedecor n'est pas significatif :
ddl = nu = (n1-1) + (n2-1)
Si le test de Snedecor est significatif le ddl est :
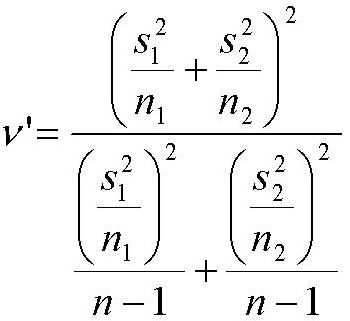
nu' est en général un nombre à virgule. On arrondit alors au nombre entier juste inférieur.
Nous sommes maintenant munis du t calculé et du degré de liberté. On choisit alors un seuil de signification (en général 0.05 ou 0.01), et on va chercher dans une table des t de Student la valeur limite correspondante au seuil et au ddl. Cette valeur limite est celle à partir de laquelle le hasard a peu de chance de donner une valeur.
Dans le cas d'une hypothèse faible, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi.
Dans le cas d'une hypothèse forte et que la différence entre les moyennes va dans le sens de celle prédite par l'hypothèse, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi multiplié par 2.
Si le seuil choisi est 0.05, on regardera la colonne 0.10.
Si on ne dispose pas d'une table de t de Student, on peut trouver ces valeurs avec un tableur (type Excel et probablement OpenCalc). On fait :
Insérer/fonction/LOI.STUDENT.INVERSE qui demande le seuil et le ddl
ou on écrit dans une cellule :
=LOI.STUDENT.INVERSE(seuil;ddl)
Par exemple : "=LOI.STUDENT.INVERSE(0.05;12)" donne 2,179
Si nous testons une hypothèse unilatérale (forte), on entrera
"=LOI.STUDENT.INVERSE(0.10;12)" qui donnera 1,782
On peut maintenant comparer le t calculé au t de la table :
Si le t calculé est supérieur à celui de la table (il dépasse la limite) le résultat a donc peu de chances d'être dû au hasard, on considère donc la différence de moyennes comme significative au seuil choisi.
Si le t calculé est inférieur à celui de la table, le résultat obtenu a pu être obtenu par hasard, et donc on ne peut pas considérer au seuil de confiance voulu que l'effet est dû au facteur étudié.
Groupe 1 : 3, 5, 5, 6, 6, 8, 10
Groupe 2 : 6, 7, 9, 9, 9, 10, 12
___________________________
Utilisation d'un logiciel (Systat)
Les résultats ont été introduits dans le logiciel comme indiqué dans la rubrique "Logiciels".
*************************************
Group N Mean SD
G1 7 6.143 2.268
G2 7 8.857 1.952
Separate Variance t = -2.400 df = 11.7 Prob = 0.034
Difference in Means = -2.714 95.00% CI = -5.184 to -0.244
Pooled Variance t = -2.400 df = 12 Prob = 0.034
Difference in Means = -2.714 95.00% CI = -5.178 to -0.250
*************************************
Nous voyons qu'il y a 2 résultats : 1 avec Separate Variance, et l'autre avec Pooled
Les variances étaient elles différentes ?
(Normalement...) Nous avons fait le test de Snedecor pour savoir si l'on peut considérer les variances comme égales ou si elles diffèrent trop (test significatif).
Si les variances sont considérées comme identiques, on lira "Pooled". Sinon, on lira "Separate". Car si elles sont trop différentes, on doit corriger le degré de liberté. C'est la raison pour laquelle nous avons df=11.7 (cas corrigé) dans un cas et df=12 dans l'autre (df = degree of freedom = degré de liberté = ddl = nu = ...).
(En réalité...) Nous n'avons pas fait le test de Snedecor. Si le df de Separate est très différent de celui de Pooled, on prendra celui de separate (simplement car le logiciel apporte la correction juste nécessaire dans Separate avec la formule de Welsch et que lorsque les variances sont identiques, cette correction est nulle).
Si on constate que la probabilité est la même (ici 0.034), c'est qu'il est inutile de prendre la version "Separate".
L'hypothèse est elle forte ou faible ?
Cas de l'hypothèse faible : le risque d'erreur alpha (risque que si le facteur n'a pas d'effet, on trouve une telle différence de moyenne à cause du hasard de l'échantillonnage) est 0.034 (3,4%). On considère que c'est significatif car c'est inférieur à 5% (une telle différence n'a que 3,4% de chance de se produire si le facteur n'a en réalité pas d'effet, donc je l'attribue à l'effet du facteur). On peut conclure au risque d'erreur alpha de 3.4% que le traitement appliqué à G2 augmente la valeur de sa VD par rapport à G1.
Cas de l'hypothèse forte MeanG1>MeanG2 : je constate que c'est le contraire qui se produit (6.143<8.857). L'analyse s'arrête ici car l'hypothèse est unilatérale, je ne peux pas dire que le traitement reçu par G1 augmente la valeur de sa VD par rapport à G2... il faut comprendre ce qui a pu se passer pendant l'expérience, revoir la théorie, formuler de nouvelles hypothèses, refaire une expérience...
Cas de l'hypothèse forte MeanG1<MeanG2 : je constate que 6.143<8.857 et que les chances d'obtenir une telle différence par hasard est de 1,7%... (0.034/2 = 0.017, car l'hypothèse est unilatérale).
Je peux conclure, au risque d'erreur alpha de 1,7% que le traitement appliqué à G2 augmente la valeur de sa VD par rapport à G1.
___________________________
Version "fait à la main"
Je calcule m1, m2, E(V1), E(V2), je connais n1 et n2
m1 = 6.143; m2 = 8.857; E(V1) = 5.14; E(V2) = 3.81
Je calcule :
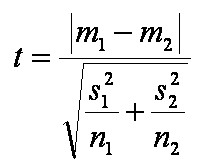
Je trouve : t = 2,4
Degrés de liberté :
Si le test de Snedecor n'est pas significatif :
ddl = nu = (n1-1) + (n2-1)
Si le test de Snedecor est significatif le ddl est :
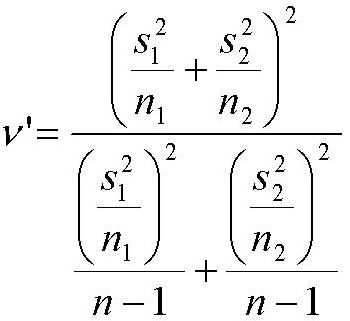
nu' est en général un nombre à virgule. On arrondit alors au nombre entier juste inférieur.
Nous sommes maintenant munis du t calculé et du degré de liberté. On choisit alors un seuil de signification (en général 0.05 ou 0.01), et on va chercher dans une table des t de Student la valeur limite correspondante au seuil et au ddl. Cette valeur limite est celle à partir de laquelle le hasard a peu de chance de donner une valeur.
Dans le cas d'une hypothèse faible, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi.
Dans le cas d'une hypothèse forte et que la différence entre les moyennes va dans le sens de celle prédite par l'hypothèse, le t limite est la valeur située à l'intersection entre la ligne du degré de liberté et la colonne du seuil choisi multiplié par 2.
Si le seuil choisi est 0.05, on regardera la colonne 0.10.
Si on ne dispose pas d'une table de t de Student, on peut trouver ces valeurs avec un tableur (type Excel et probablement OpenCalc). On fait :
Insérer/fonction/LOI.STUDENT.INVERSE qui demande le seuil et le ddl
ou on écrit dans une cellule :
=LOI.STUDENT.INVERSE(seuil;ddl)
Par exemple : "=LOI.STUDENT.INVERSE(0.05;12)" donne 2,179
Si nous testons une hypothèse unilatérale (forte), on entrera
"=LOI.STUDENT.INVERSE(0.10;12)" qui donnera 1,782
On peut maintenant comparer le t calculé au t de la table :
Si le t calculé est supérieur à celui de la table (il dépasse la limite) le résultat a donc peu de chances d'être dû au hasard, on considère donc la différence de moyennes comme significative au seuil choisi.
Si le t calculé est inférieur à celui de la table, le résultat obtenu a pu être obtenu par hasard, et donc on ne peut pas considérer au seuil de confiance voulu que l'effet est dû au facteur étudié.
Retour aux articles de la catégorie Stats : choisir son test -
⨯
Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 74 autres membres