NeuropsychoJolly (roger)

La deuxième solution consiste à utiliser les statistiques.
L'objectif de cette page est de montrer que nous pratiquons déjà les statistiques automatiquement, sans le savoir.

Si le groupe rouge reçoit la drogue promnésiante et le bleu le solvant correspondant, et que l'on mesure la performance mnésique, est-on tenté de dire que la drogue a un effet dans le premier cas ? Est-on tenté de dire que la drogue a un effet dans le deuxième cas ?



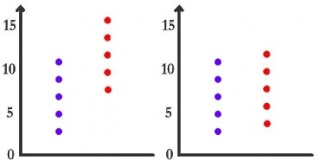
Je pense que ce sera oui pour le premier cas et non pour le second. Qu'est-ce qui diffère entre ces deux cas ?


Est-on tenté de dire que la drogue a un effet dans le cas 3 ? Est-on tenté de dire que la drogue a un effet dans le cas 4 ?



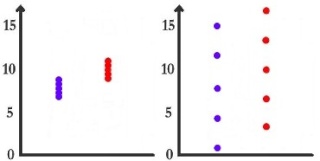
Je pense que ce sera oui pour le cas 3 et non pour le cas 4. A nouveau, qu'est-ce qui diffère entre ces deux cas ?

Enfin, est-on tenté de dire que la drogue a un effet dans le cas 5 ? Est-on tenté de dire que la drogue a un effet dans le cas 6 ?



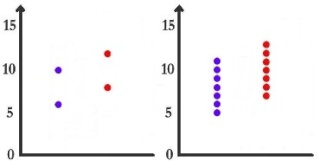
Je pense que ce sera oui pour le cas 5 et non pour le cas 6. La conclusion nous paraît cependant normalement plus litigieuse dans cette dernière situation. Disons que si je devais investir dans la production du médicament testé dans les conditions du cas 6, j'aurais plus confiance que dans la solution du cas 5. Une dernière fois, qu'est-ce qui diffère entre ces deux cas ?


On conviendra que dans la première situation, c'est l'amplitude de la différence des moyennes qui a facilité notre décision. Dans la deuxième situation (cas 3 net 4), c'est le fait que les résultats étaient moins variables dans le cas 3 que dans le 4, car la différence de moyennes était la même. Enfin, la dernière situation nous permet de constater que les effectifs importants facilitent également notre décision par rapport aux effectifs faibles.

Si vous montrez ces différents graphiques, un par un,  à plusieurs personnes et que vous leurs demandez si d'après eux, la drogue a un effet ou non, vous obtiendrez des réponses différentes. Mais plus on augmente la différence entre les deux moyennes, plus la réponse fait l'unanimité.
Notre but est maintenant de trouver un critère qui permette de mettre tout le monde d'accord. Or, c'est également l'objet des tests statistiques.
Comme nous le verrons plus tard, le test statistique le plus célèbre (le t de Student) est celui qui permet de traiter ce type de problème.

Or, celui-ci se base exactement sur ces trois paramètres (amplitude de la différence de moyennes, variabilité et effectif)  pour nous aider à analyser nos données.

Avant de nous lancer dans l'étude de ce test, nous devons faire quelques remarques.

Pourquoi l'effectif facilite-t-il notre décision ?
- dans le cas 6, tous les sujets sont "rangés" entre deux extrèmes. On imagine que si on en ajoutait d'autres, ils viendraient également se placer à part quelques exceptions, entre ces deux extrèmes. A l'inverse, dans le cas 5, on n'est sûr de rien.
- cela signifie qu'implicitement, on sait que les sujets que l'on observe sont censés "représenter" une population plus large. Ainsi, on tente d'inférer  les caractéristiques d'une population à partir d'un échantillon.
Plus l'effectif est important, plus il a de chances de ressembler à la population totale. C'est la raison pour laquelle augmenter l'effectif facilite notre décision.
Cela conforte l'idée que lorsque je teste un nouveau médicament, le groupe de sujet sur lequel je travaille ne m'intéresse que parce qu'il représente une population beaucoup plus vaste.

Pourquoi une faible variabilité facilite-t-elle notre décision ?
- pour la même raison : on imagine que si on ajoutait d'autres sujets, et que la variabilité observée dans chaque groupe représente la variabilité de la population dont ils sont issus, les nouveaux points viendraient également se placer, à part quelques exceptions, entre les deux extrêmes.

Que cherchons nous réellement à inférer dans ces populations ?
Tout simplement leurs moyennes (car la différence entre ces moyennes reflète le bénéfice induit par la drogue).

Puisque notre but est de trouver un critère qui permette de mettre tout le monde d'accord, nous allons maintenant quantifier la moyenne et la variabilité des échantillons, et tenter d'estimer à partir de ces échantillons, les moyennes et variabilités des populations dont sont extraits ces échantillons.

Page suivante : Moyenne d'un échantillon et moyenne de la population
Page précédente : Première solution : la roulette de Monte-Carlo
Retour au plan